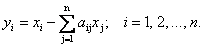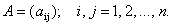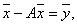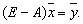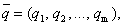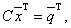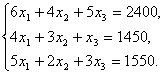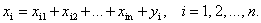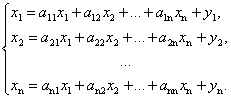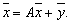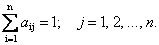Высшая математика в экономике
Одним из примеров экономического процесса, приводящего к понятию собственного числа и собственного вектора матрицы, является процесс взаимных закупок товаров. Будем полагать, что бюджеты п стран, которые мы обозначим соответственно x1, x2, … , xn расходуются на покупку товаров. Мы будем рассматривать линейную модель обмена, или, как ее еще называют, модель международной торговли.
Пусть aij — доля бюджета xj, которую j-я страна тратит на закупку товаров у i-й страны. Введем матрицу коэффициентов aij:
Тогда если весь бюджет расходуется только на закупки внутри страны и вне ее (можно это трактовать как торговый бюджет), то справедливо равенство
Матрица (16.12) со свойством (16.13), в силу которого сумма элементов ее любого столбца равна единице, называется структурной матрицей торговли. Для i-й страны общая выручка от внутренней и внешней торговли выражается формулой
Условие сбалансированной (бездефицитной) торговли формулируется естественным образом: для каждой страны ее бюджет должен быть не больше выручки от торговли, т.е. Pi ≥ xi:, или
Докажем, что в условиях (16.14) не может быть знака неравенства. Действительно, сложим все эти неравенства при i от 1 до n. Группируя слагаемые с величинами бюджетов xj, получаем
Нетрудно видеть, что в скобках стоят суммы элементов матрицы А по ее столбцам от первого до последнего, которые равны единице по условию (16.13). Стало быть, мы получили неравенство
откуда возможен только знак равенства.
Таким образом, условия (16.14) принимают вид равенств:
Введем вектор бюджетов 
, каждая компонента которого характеризует бюджет соответствующей страны; тогда систему уравнений (16.15) можно записать в матричной форме
Это уравнение означает, что собственный вектор структурной матрицы А, отвечающий ее собственному значению λ = 1, состоит из бюджетов стран бездефицитной международной торговли.
Перепишем уравнение (16.16) в виде, позволяющем определить :
Пример. Структурная матрица торговли четырех стран имеет вид:
Найти бюджеты этих стран, удовлетворяющие сбалансированной бездефицитной торговле при условии, что сумма бюджетов задана:
Решение. Необходимо найти собственный вектор , отвечающий собственному значению λ = 1 заданной структурной матрицы А, т.е. решить уравнение (16.17), которое в нашем случае имеет вид
Поскольку ранг этой системы равен трем, то одна из неизвестных является свободной переменной и остальные выражаются через нее. Решая систему методом Гаусса, находим компоненты собственного вектора :
Подставив найденные значения в заданную сумму бюджетов, найдем величину с: с = 1210, откуда окончательно получаем искомые величины бюджетов стран при бездефицитной торговле (в условных денежных единицах):
16.1. По данным табл. 16.1 составить новую таблицу производственно-экономических показателей по следующим условиям:
— количество изделий всех видов увеличивается на 20%,
— норма времени изготовления по всем изделиям уменьшается на 20%,
— цена на все виды изделий уменьшается на 10%.
Найти ежесуточные показатели, указанные в задаче 1 п. 16.1, а также их процентные изменения.
16.2. По данным табл. 16.2 составить новую таблицу по следующим условиям:
— дневная производительность всех предприятий увеличивается на 100%,
— число рабочих дней в году для 1-го предприятия увеличивается на 50%, а для остальных — на 40%,
— цены на виды сырья уменьшаются соответственно на 10, 20 и 30%.
Определить суммы кредитования предприятий и их соответствующие процентные изменения.
16.3. Отрасль состоит из 4-х предприятий; вектор выпуска продукции и матрица внутреннего потребления имеют вид
Найти вектор объемов конечного продукта, предназначенного для реализации вне отрасли.
16.4. Предприятие выпускает три вида продукции с использованием трех видов сырья, характеристики производства указаны в следующей таблице:
Найти объем выпуска продукции каждого вида при заданных запасах сырья.
16.5. В условиях примера 2 п. 16.2 определить прирост объемов валовых выпусков по каждой отрасли (в процентах), если конечное потребление увеличить по отраслям соответственно на 30, 10 и 50%. Решить задачу методом обратной матрицы и методом Гаусса.
16.6. Структурная матрица торговли трех стран имеет вид
Найти бюджеты первой и второй стран, удовлетворяющие сбалансированной бездефицитной торговле при условии, что бюджет третьей страны равен 1100 усл. ед.
Пример. Найти производную функции
.
Сначала преобразуем данную функцию: 
Пример. Найти производную функции 
.
Пример. Разложить в ряд функцию 
Разложение в ряд этой функции по формуле Маклорена было рассмотрено выше.
(См. Функция y= ln (1 + x)) Теперь решим эту задачу при помощи интегрирования.
При 
получаем по приведенной выше формуле:
Разложение в ряд функции 
может быть легко найдено способом алгебраического деления аналогично рассмотренному выше примеру.
Тогда получаем: 
Окончательно получим: 
Источник
2.6. Линейная модель международной бездефицитной торговли
Будем считать, что бюджеты (X1; X2; …Xn) N стран расходуются этими странами целиком на покупку товаров внутри страны и вне ее (так называемый торговый бюджет). И пусть Xij – сумма, на которую J-ая страна закупает товаров у I-ой страны. Тогда
(J = 1, 2,… N) (3.10)
– бюджет J-ой страны, а
(I = 1, 2,… N) (3.11)
– общая выручка I-ой страны от внутренней и внешней торговли. При торговом бездефицитном бюджете общая выручка страны и составляет ее бюджет. Поэтому
(I = 1, 2,… N) (3.12)
(I,J = 1, 2,… N) (3.13)
– доля бюджета Xj, которую тратит J-ая страна на закупку товаров у I-ой страны. Тогда
(I,J = 1, 2,… N), (3.14)
Причем, в силу (3.10) и (3.13),
(J = 1, 2,… N), (3.15)
Подставляя выражения (3.14) для Xij в выражения (3.11) для Pi и учитывая равенства (3.12), приходим к системе и линейных уравнений с N неизвестными (X1; X2; …Xn):
(I = 1, 2,… N), (3.16)
Или, в развернутой форме, к системе:
(3.17)
(3.18)
Коэффициентов системы (3.18) называется Матрицей структурной торговли. Ее особенностью, согласно (3.15), является то, что сумма элементов каждого ее столбца равна единице, и все ее элементы неотрицательны. Если она задана, то решив систему (3.17), найдем бюджеты (X1; X2; …Xn) всех стран, принимающих участие в бездефицитной торговле.
Отметим, что система (3.17) является однородной. Действительно, перенеся правые части в (3.17) налево, получим следующую однородную систему
(3.19)
Сложив все уравнения этой системы, в силу равенств (3.15) получим тождество 
. Это значит, что каждое отдельное уравнение системы (3.19) можно выразить через другие ее уравнения. То есть каждое уравнение системы (3.19) является следствием остальных. Иначе говоря, оно автоматически будет выполняться, если будут выполняться остальные N–1 уравнений. Но это значит, что в системе (3.19) одно уравнение (любое!) можно отбросить. Тогда вместо квадратной системы (3.19) получим недоопределенную однородную систему. А недоопределенная система, как мы знаем из § 1, может или иметь бесчисленное множество решений, или не иметь их вообще. Но не иметь решений она не может, ибо заведомо одно решение (тривиальное) у нее есть: (
; 
; …; 
). Значит, система (3.19) имеет бесчисленное множество решений. Чтобы из этого множества выделить искомое решение (X1; X2; …Xn), необходимо задать некоторое дополнительное условие для ее неизвестных, то есть для бюджетов Xi (I = 1, 2,… N) всех стран. Например, задать суммарный бюджет С Всех стран:
(3.20)
Пример 2. Структурная матрица торговли четырех стран имеет вид:
Найти бюджеты (X1; X2; X3; X4) этих стран, удовлетворяющие сбалансированной бездефицитной торговле при условии, что сумма бюджетов задана:
(усл. ед.).
Решение. Составим систему (3.19):
Отбросив в этой системе последнее уравнение и решив оставшуюся систему методом Гаусса (выкладки опускаем), получим:
; 
; 
; 
,
Где T – свободный (произвольный) параметр. Подставив эти выражения в заданную сумму бюджетов, определим величину T:
1. В таблице приведены данные об исполнении межотраслевого баланса за некоторый отчетный период в условных денежных единицах:
Источник
Применение линейной алгебры в экономике
Производственные показатели
Предприятие выпускает ежесуточно четыре вида изделий, основные производственно-экономические показатели которых приведены в следующей таблице:
изделия, ден. ед./изд.
Требуется определить следующие ежесуточные показатели: расход сырья S , затраты рабочего времени Т и стоимость Р выпускаемой продукции предприятия.
По приведенным данным составим четыре вектора, характеризующие весь производственный цикл:
= (20, 50, 30, 40) — вектор ассортимента;
= (5, 2, 7, 4) — вектор расхода сырья;
= (10, 5, 15, 8) — вектор затрат рабочего времени;
= (30, 15, 45, 20) — ценовой вектор.
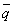
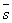
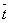
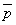
Тогда искомые величины будут представлять собой соответствующие скалярные произведения вектора ассортимента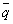 
на три других вектора:
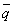
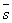
S = = 100 + 100 + 210 + 160 = 570 кг ,
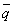
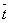
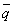
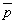
Т = = 1220 ч, P = 
= 3500 ден. ед.
Расход сырья
Предприятие выпускает четыре вида изделий с использованием четырех видов сырья. Нормы расхода сырья даны как элементы матрицы А:
Вид сырья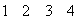 
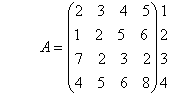
Вид изделия.
Требуется найти затраты сырья каждого вида при заданном плане выпуска каждого вида изделия: соответственно, 60, 50, 35 и 40 ед.
Составим вектор-план выпуска продукции:
=(60, 50, 35, 40).
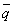
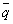
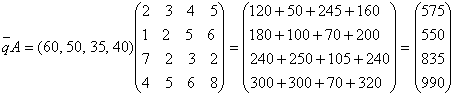
Тогда решение задачи дается вектором затрат, координаты которого и являются величинами затрат сырья по каждому его виду: этот вектор затрат вычисляется как произведение вектора на матрицу А:
.
Конечный продукт отрасли
Отрасль состоит из п предприятий, выпускающих по одному виду продукции каждое: обозначим объем продукции i -го предприятия через х i . Каждое из предприятий отрасли для обеспечения своего производства потребляет часть продукции, выпускаемой им самим и другими предприятиями. Пусть а ij — доля продукции i -го предприятия, потребляемая j-м предприятием для обеспечения выпуска своей продукции объема х j . Найдем величину у i — количество продукции i-го предприятия, предназначенной для реализации вне данной отрасли (объем конечного продукта). Эта величина легко может быть подсчитана по формуле
Введем в рассмотрение квадратную матрицу порядка п, описывающую внутреннее потребление отрасли
Тогда вектор конечного продукта является решением матричного уравнения
с использованием единичной матрицы Е получаем
Пример. Пусть вектор выпуска продукции отрасли и матрица внутреннего потребления имеют, соответственно, вид
.
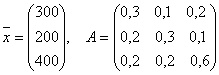
Получим вектор объемов конечного продукта, предназначенного для реализации вне отрасли, состоящей из трех предприятий:
.
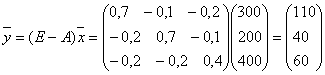
Прогноз выпуска продукции
Пусть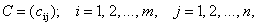 
— матрица затрат сырья т видов при выпуске продукции п видов. Тогда при известных объемах запаса каждого вида сырья, которые образуют соответствующий вектор
вектор-план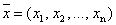 
выпуска продукции определяется из решения системы т уравнений с п неизвестными:
где индекс «т» означает транспонирование вектора-строки в вектор-столбец.
Пример. Предприятие выпускает три вида продукции, используя сырье трех видов. Необходимые характеристики производства представлены следующими данными:
Вид сырья
Расход сырья по видам
продукции, вес. ед./изд.
Требуется определить объем выпуска продукции каждого вида при заданных запасах сырья.
Задачи такого рода типичны при прогнозах и оценках функционирования предприятий, экспертных оценках проектов освоения месторождений полезных ископаемых, а также в планировании микроэкономики предприятий.
Обозначим неизвестные объемы выпуска продукции через х 1 , х 2 и х 3 . Тогда при условии полного расхода запасов каждого вида сырья можно записать балансовые соотношения, которые образуют систему трех уравнений с тремя неизвестными:
Решая эту систему уравнений любым способом, находим, что при заданных запасах сырья объемы выпуска продукции составят по каждому виду соответственно (в условных единицах):
.
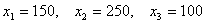
Линейная модель многоотраслевой экономики
Для простоты будем полагать, что производственная сфера хозяйства представляет собой п отраслей, каждая из которых производит свой однородный продукт. Для обеспечения производства каждая отрасль нуждается в продукции других отраслей (производственное потребление). Обычно процесс производства рассматривается за некоторый период; в ряде случаев такой единицей служит год.
Введем следующие обозначения:
— общий объем продукции i -й отрасли;
— объем продукции i-й отрасли, потребляемый j -й отраслью при производстве объема продукции 
;
— объем продукции i -й отрасли, предназначенный для реализации (потребления) в непроизводственной сфере, или так называемый продукт конечного потребления.
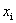
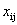
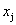
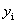
Балансовый принцип связи различных отраслей промышленности состоит в том, что валовой выпуск i -й отрасли должен быть равен сумме объемов потребления в производственной и непроизводственной сферах. В самой простой форме (гипотеза линейности, или простого сложения) балансовые соотношения имеют вид
Эти уравнения называются соотношениями баланса. Поскольку продукция разных отраслей имеет разные измерения, в дальнейшем будем иметь в виду стоимостный баланс.
В. Леонтьевым на основании анализа экономики США в период перед второй мировой войной был установлен важный факт: в течение длительного времени величины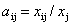 
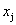
меняются очень незначительно и могут рассматриваться как постоянные числа. Это явление становится понятным в свете того, что технология производства остается на одном и том же уровне довольно длительное время, и, следовательно, объем потребления j -й отраслью продукции i -й отрасли при производстве своей продукции объема есть технологическая константа.
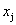
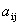
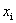
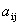
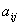
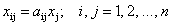
В силу указанного факта можно сделать следующее допущение: для производства продукции j -й отрасли объема нужно использовать продукцию i -й отрасли объема 
, где — постоянное число. При таком допущении технология производства принимается линейной, а само это допущение называется гипотезой линейности. При этом числа 
называются коэффициентами прямых затрат. Согласно гипотезе линейности
.
Соотношения баланса можно переписать в виде системы уравнений
Введем в рассмотрение векторы-столбцы объемов произведенной продукции (вектор валового выпуска), объемов продукции конечного потребления (вектор конечного потребления) и матрицу коэффициентов прямых затрат:
.
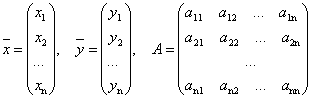
Тогда система уравнений в матричной форме имеет вид
Обычно это соотношение называют уравнением линейного межотраслевого баланса. Вместе с описанием матричного представления это уравнение носит название модели Леонтьева.
Уравнение межотраслевого баланса можно использовать в двух целях. В первом (наиболее простом) случае, когда известен вектор валового выпуска 
, требуется рассчитать вектор конечного потребления 
. Во втором случае уравнение межотраслевого баланса используется для целей планирования со следующей формулировкой задачи: для периода Т (например, год) известен вектор конечного потребления , требуется определить вектор валового выпуска.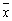
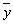
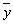
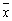
Линейная модель торговли
Процесс взаимных закупок товаров анализируется с использованием понятий собственного числа и собственного вектора матрицы. Будем полагать, что бюджеты n стран, которые мы обозначим, соответственно, х 1 , х 2 , …, х n , расходуются на покупку товаров. Рассмотрим линейную модель обмена, или модель международной торговли.
Пусть а ij — доля бюджета х j , которую j -я страна тратит на закупку товаров у i —й страны. Введем матрицу коэффициентов а ij :
.
Тогда, если весь бюджет расходуется только на закупки внутри страны и вне ее (это можно трактовать как торговый бюджет), справедливо равенство
Матрица А с данным свойством, в силу которого сумма элементов ее любого столбца равна единице, называется структурной матрицей торговли. Для i -й страны общая выручка от внутренней и внешней торговли выражается формулой
.
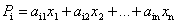
Условие сбалансированной (бездефицитной) торговли формулируется естественным образом: для каждой страны ее бюджет должен быть не больше выручки от торговли, т.е.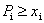 
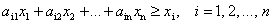
, или
.
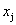
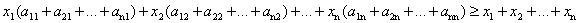
Докажем, что в условиях не может быть знака неравенства. Действительно, сложим все эти неравенства при i от 1 до п. Группируя слагаемые с величинами бюджетов , получаем
.
Нетрудно заметить, что в скобках стоят суммы элементов матрицы А по ее столбцам, которые равны единице по условию. Стало быть, мы получили неравенство
,
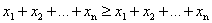
откуда следует, что возможен только знак равенства.
Таким образом, условия принимают вид равенств:
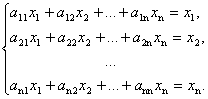
Введем вектор бюджетов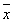 
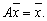
, каждая компонента которого характеризует бюджет соответствующей страны. Тогда систему уравнений можно записать в матричной форме:
Это уравнение означает, что собственный вектор структурной матрицы А, отвечающий ее собственному значению l =1, состоит из бюджетов стран бездефицитной международной торговли. Перепишем уравнение в виде, позволяющем определить :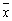
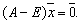
Пример. Структурная матрица торговли четырех стран имеет вид
.
Найти бюджеты этих стран, удовлетворяющие сбалансированной бездефицитной торговле при условии, что сумма бюджетов задана:
.
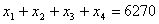
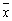
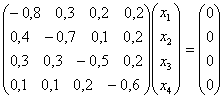
Решение. Необходимо найти собственный вектор , отвечающий собственному значению l =1 заданной структурной матрицы А, т.е. решить уравнение, которое в нашем случае имеет вид
.
Поскольку ранг этой системы равен трем, то одна из неизвестных является свободной переменной, остальные выражаются через нее. Решая систему методом Гаусса, находим компоненты собственного вектора :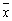
.
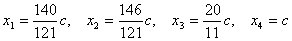
Подставив найденные значения в заданную сумму бюджетов, определим величину с:
Откуда окончательно получаем искомые величины бюджетов стран при бездефицитной торговле:
.
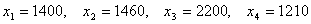
Источник
