Как найти страны прямоугольника

Стороны прямоугольника

Свойства

Зная стороны прямоугольника, можно вычислить все остальные его параметры, используя следующий ход действий. Периметр прямоугольника представляет собой удвоенную сумму его сторон, поэтому его можно сразу вычислить. P=2(a+b)

Площадь прямоугольника равна произведению его сторон, поэтому ее также можно найти сразу. S=ab

Диагонали в прямоугольнике являются конгруэнтными, каждая из них образует прямоугольный треугольник со сторонами прямоугольника. Из теоремы Пифагора каждая диагональ будет равна квадратному корню из суммы квадратов сторон прямоугольника. (рис. 56.1) d_1=d_2=√(a^2+b^2 )

Из этого же прямоугольного треугольника можно найти углы α и β при диагоналях, зная только стороны прямоугольника. Отношения катетов друг к другу дают тангенс или котангенс углов треугольника, поэтому α и β будут равны арктангенсу отношений сторон, а дальше значение в градусах можно найти, используя таблицы тангенсов. α=arc tan⁡〖b/a〗 β=arc tan⁡〖a/b〗

Углы γ и δ, образованные пересечением диагоналей, как видно из чертежа, через прямоугольный треугольник с полуосью, равны удвоенным значениям α и β соответственно. (рис.56.2) γ=2α δ=2β

Так как углы у прямоугольника все равны друг другу, вокруг него можно описать окружность. Центр окружности будет находиться в точке пересечения диагоналей, и следовательно, радиус описанной окружности будет равен половине диагонали. (рис.56.3) R=d/2=√(a^2+b^2 )/2

Источник

Cтороны прямоугольника

Длины прямоугольника

Очень часто понятия длины и ширины путаются. Некоторые источники утверждают, что вертикальные стороны прямоугольника – это ширина. Но это редкость, обычно длиной называется большая сторона прямоугольника, а шириной меньшая.

Для лучшего восприятия стоит располагать фигуру так, чтобы длина находилась в основании, а боковые стороны имели размеры ширины. Так будет проще решать задачи.

Перед тем, как перейти непосредственно к решению задач, нужно повторить несколько фактов, которые облегчат решение:

• Диагонали прямоугольника равны.
• Диагонали точкой пересечения делятся пополам.
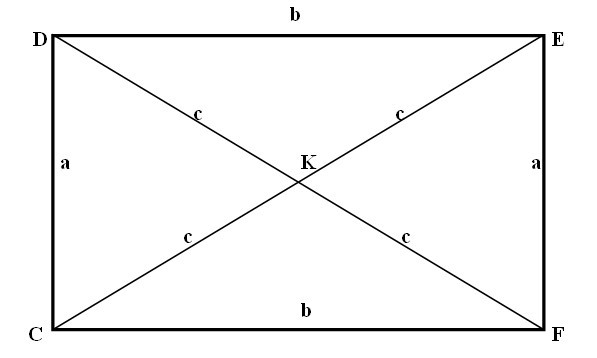
• Диагонали прямоугольника делят прямоугольник на 4 равнобедренных треугольника, которые равны между собой.

Рис. 1. Прямоугольник

Примеры решения задач

Решим задачу, связанную с формулами вычисления сторон прямоугольника. Рассмотрим несколько вариантов нахождения длин сторон при различных известных параметрах.

Задача 1

• Известно, что площадь прямоугольника равна 21, а периметр 20. Найти стороны прямоугольника.

Такая задача содержит две неизвестных. Величины сторон a и b. Чтобы найти оба значения необходимо составить систему уравнений:

$(a+b)*2=P$ (уравнение нахождения периметра как суммы сторон фигуры)

$a*b=S$ (уравнение для нахождения площади)

При наличии двух неизвестных для решения системы необходимо наличие двух уравнений. Поэтому невозможно найти стороны прямоугольника, зная только площадь или только периметр.

Продолжим решение. Выразим значение a из первого выражения системы.

Подставим получившееся выражение в уравнение нахождения площади:

Это квадратное уравнение. Решим его с помощью теоремы Виета. Такое уравнение будет иметь два корня. Сумма корней будет равна 10, а произведение 21. Такое возможно при значении корней 3 и 7, так как это единственные числа, подходящие под данные условия.

Значит, при $b=3$, $а=10-3=7$

При $b=7$, $a=10-7=3$. То есть в любом случае, стороны будут равны 7 и 3. Это и есть ответ задачи.

Задача 2

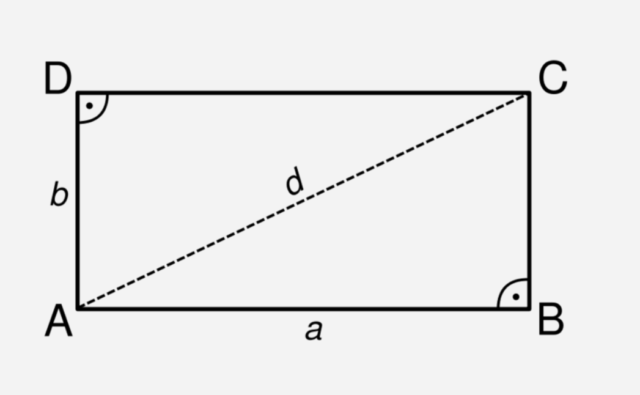
• Известно, что сторона прямоугольника равна 16, а диагональ 20. Найти другую сторону прямоугольника.

Рис. 2. Рисунок к задаче.

Задача решается теоремой Пифагора. Диагональ делит прямоугольник на два равных прямоугольных треугольника. В таком треугольнике нам известна гипотенуза (20) и катет (16).

Сумма квадратов катетов равняется квадрату гипотенузы. Искать будем сторону а, предположив, что известная нам сторона это сторона b.

Корень квадратный из 144 равен 12. Это и есть ответ к задаче.

Задача 3

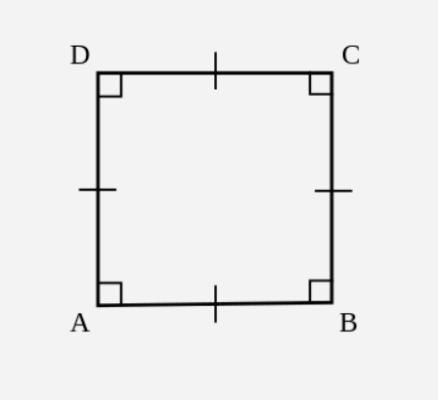
• Известно, что прямоугольник представляет собой ромб. Площадь ромба равна 25, необходимо найти все стороны четырехугольника.

У прямоугольника все углы прямые, а у ромба все стороны между собой равны. Значит, четырехугольник, который одновременно является и ромбом, и прямоугольником это фигура с 4 прямыми углами и сторонами, равными между собой. Такой фигурой может быть только квадрат.

Стороны квадрата равны, значит нас интересует одно значение. Площадь квадрата это значение стороны, возведенное в квадрат.

Что мы узнали?

Мы узнали, как найти длины прямоугольника. Рассмотрели различные типовые ситуации и научились решать задачи, связанные с нахождением длин прямоугольника.

Тест по теме

• Квадрат со стороной 4
• Квадрат со стороной 8
• Никак, это простой прямоугольник
• Это не прямоугольник

Оценка статьи

Средняя оценка: 4.4 . Всего получено оценок: 117.

• Все
• Литература
• Русский язык
• Чтение
• География
• Окружающий мир
• Физика
• Английский язык
• Биология
• Геометрия
• Алгебра
• Математика
• Обществознание
• Химия
• Информатика
• История России
• История

• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 

Не понравилось? — Напиши в комментариях, чего не хватает.

Содержание

1. Длины прямоугольника
2. Примеры решения задач
3. Задача 1
4. Задача 2
5. Задача 3
6. Что мы узнали?

Бонус

• Объем прямоугольника
• Длина прямоугольника
• Признаки прямоугольника Cтороны прямоугольника
• Признаки равенства прямоугольных треугольников
• Свойство биссектрисы треугольника
• Уравнение
• Формула
• Что такое отрезок в математике?
• Измерение углов
• Числовые выражения
• Числовые и буквенные выражения
• Диагональ треугольника
• Гипотенуза треугольника
• Основание треугольника
• Формула прямоугольника
• Cложение и вычитание: порядок выполнения
• Свойства вычитания
• Сочетательное свойство сложения
• Переместительное свойство сложения
• Сочетательный закон сложения
• Переместительный закон сложения
• Многоугольник
• Полный угол

показать все

1. 1. DExsaut 104
2. 2. Alina 100
3. 3. Алиса Туманова 93
4. 4. Юрий Острогов 80
5. 5. Ирина Любимова 61
6. 6. Игорь Проскуренко 60
7. 7. Віка Бондар 56
8. 8. Александра Апарина-Иванова 54
9. 9. Кирилл Королёв 52
10. 10. Алина Колотилова 51

1. 1. Игорь Проскуренко 23,766
2. 2. Кристина Волосочева 19,120
3. 3. Ekaterina 18,721
4. 4. Юлия Бронникова 18,580
5. 5. Darth Vader 17,856
6. 6. Алина Сайбель 16,787
7. 7. Мария Николаевна 15,775
8. 8. Лариса Самодурова 15,735
9. 9. Liza 15,165
10. 10. TorkMen 14,876

Самые активные участники недели:

• 1. Виктория Нойманн — подарочная карта книжного магазина на 500 рублей.
• 2. Bulat Sadykov — подарочная карта книжного магазина на 500 рублей.
• 3. Дарья Волкова — подарочная карта книжного магазина на 500 рублей.

Три счастливчика, которые прошли хотя бы 1 тест:

• 1. Наталья Старостина — подарочная карта книжного магазина на 500 рублей.
• 2. Николай З — подарочная карта книжного магазина на 500 рублей.
• 3. Давид Мельников — подарочная карта книжного магазина на 500 рублей.

Карты электронные(код), они будут отправлены в ближайшие дни сообщением Вконтакте или электронным письмом.

Источник