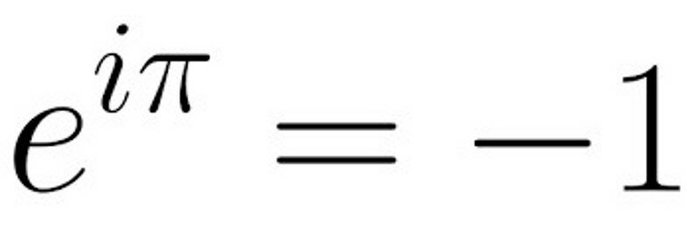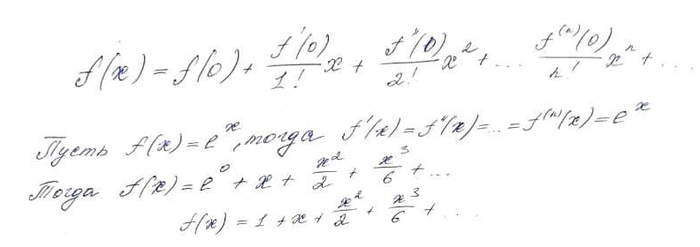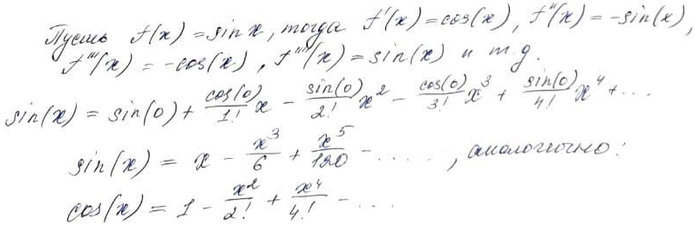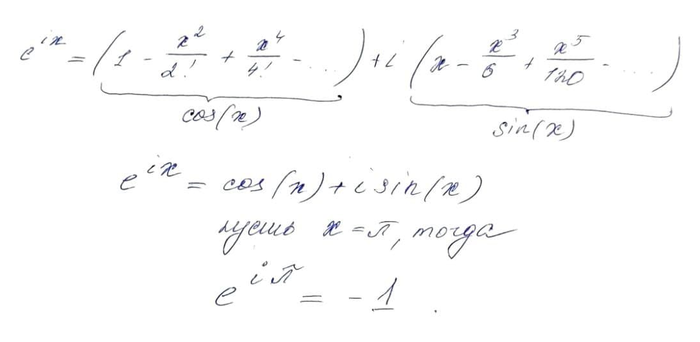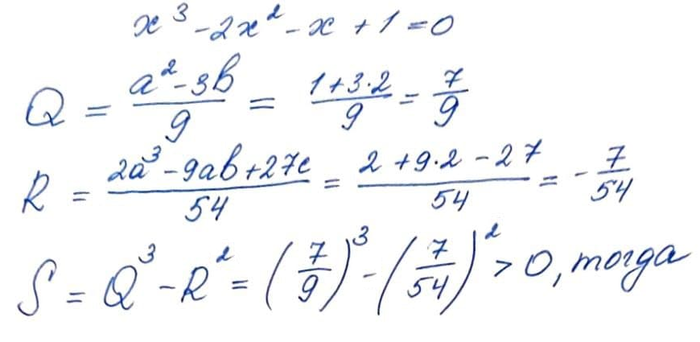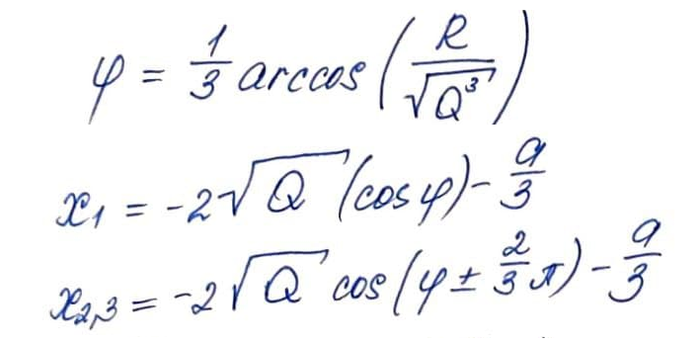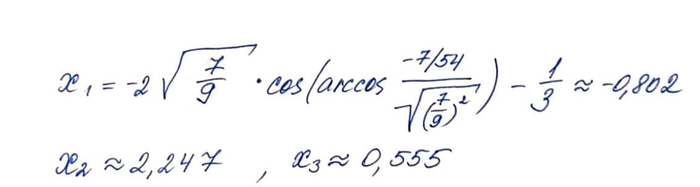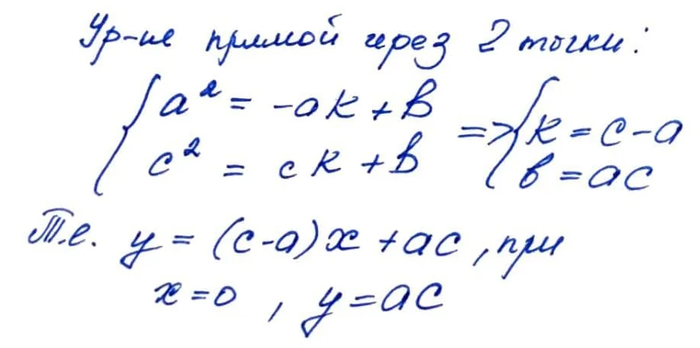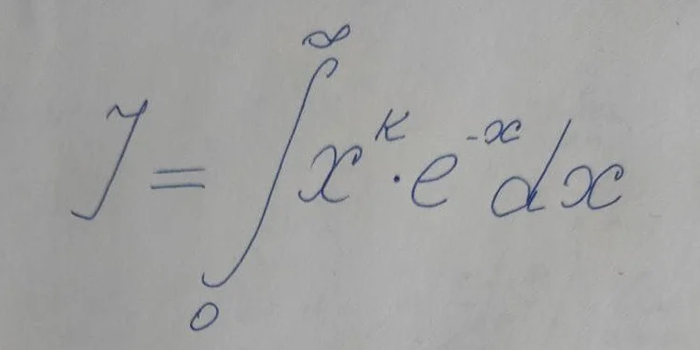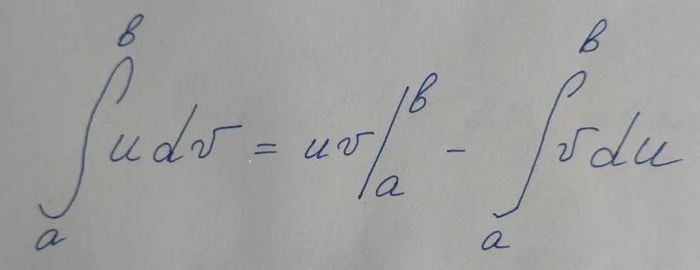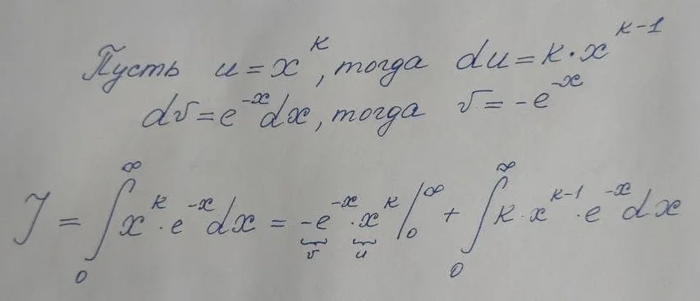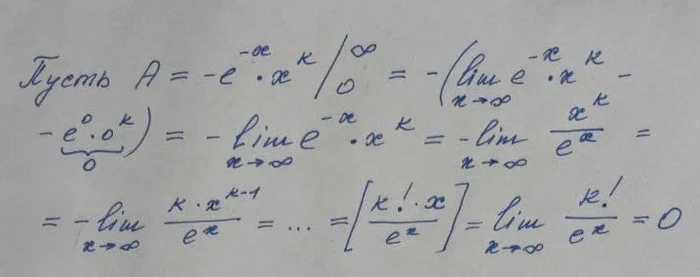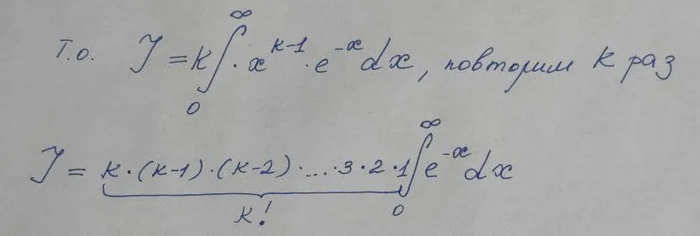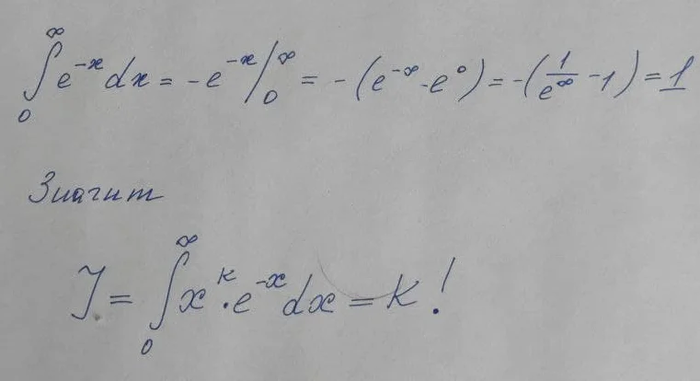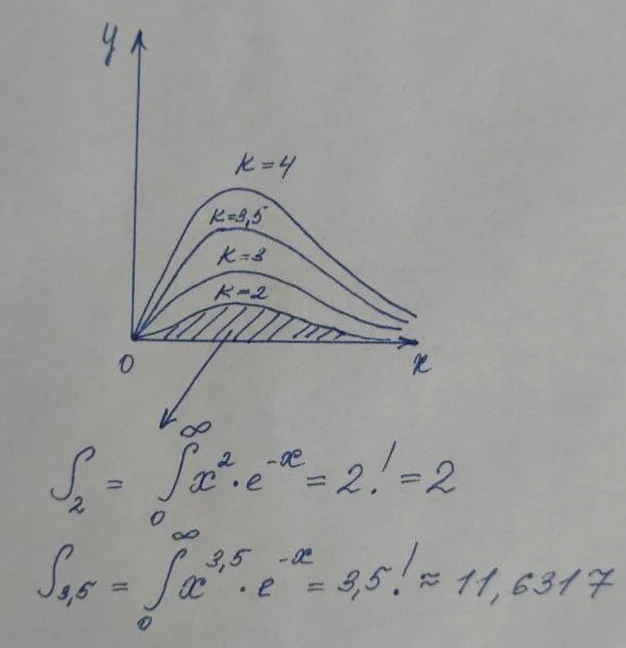Количество медалей у стран участников

У кого больше медалей за всю историю Олимпиад? ТОП 10

Сборная США выступает на олимпийских играх с 1896 года. И в отличие от некоторых стран она не распадалась, и все свои медали сохранила. Позже поясню, что имеется ввиду.

Американцы, чаще других принимали участие на олимпийских соревнованиях, пропустив только одни игры в 1980 году.

Это единственная страна, которой удалось преодолеть рубеж в тысячу золотых медалей.

В итоговой таблице на Зимних олимпиадах они были первыми лишь один раз, в то время как летом соединенные штаты финишировали во главе медального зачета 17 раз.

Данные представлены с учетом последних зимних и летних олимпийских состязаний.

Эта североамериканская страна провела 8 домашних игр (4 лета и 4 зимы), и в 2028 в Лос-Анджелесе пройдет 9 игра на территории этого государства. Последний турнир, где они хозяйничали, состоялся в 2002 году в Солт-Лейк-Сити.

Главным конкурентом американцев, в том числе и в спорте, был Советский Союз, который начал выступать лишь с 1952 года. За 36 лет страной заработано в итоге 1204 медали различного достоинства . 1010 на летних играх и 194 на зимних.

Все эти медали признаются МОК (международным комитетом), однако эта организация приняла решения не суммировать награды не существующих стран. Что имеется в виду, про это чуть позже?

У Германия 615 летних наград, а вот зимних — 240.

Этот тот самый случай, когда МОК не прибавила этой стране медали завоеванные ФРГ и ГДР. При грубом подсчете их могло быть более 1750.

Германия, как США и Великобритания, также была одной из 14-ти стран на самых первых играх.

Летние соревнования выигрывала ГДР , также им покорялась одна зимняя Олимпиада. А вот Германия побеждала зимой трижды и один раз летом.

Так как международный олимпийский комитет не суммирует достижение этих стран, запишет Германии 4 победы.

Сколько раз Германия организовывала турнир? Два раза. Оба в 1936 году в Берлине. Кроме того, на территории страны (ФРГ) в 1972 году состоялись летние игры, принимающий городом был Мюнхен. Но МОК для ФРГ ведет отдельную статистику. Про это нужно было сказать, надеюсь, я вас не запутал.

9-е место у России. Страна начала самостоятельно выступать с 1994 года, и за этот короткий промежуток пополнила свою копилку 546 наградами. 426 были летом, остальные 120 — в зимний период.

Нужно учесть, что здесь нет медалей олимпийских атлетов из России, которые выступали под нейтральным флагом.

Надо добавить одну интересную вещь, в 1992 году проходили и зимние, и летние игры, россияне выступали под объединенным флагом вместе с армянами, белорусами, азербайджанцами и другими выходцами из бывшего СССР.

И эта команда добыла за две Олимпиады 135 наград. Олимпийская сборная 1992 года с этим показателем держится на 31 месте по общему количеству медалей. Но как было сказано выше, МОК отказывается эти медали суммировать, поэтому имеем то, что имеем.

Более того, эта объединенная команда выиграла летнюю Олимпиаду . Получается вместе с СССР – 7 побед на летних играх.

10-е место в нашем списке занимает Норвегия. Но она нас ещё удивит.

В медальном зачете, который вы видите, учтены все изменения, в том числе окулированные медали по состоянию на июнь 2019 года.

Возможно, кого – то волнует вопрос, а сколько было бы сейчас медалей у Советского Союза, если бы он существовал? Если вас этот вопрос не волнует, пролистайте.

Получилась бы следующая картина. Суммируем все страны постсоветского пространства, а также медали российской империи и независимых спортсменов. Выходит 2409 наград.

К сожалению, Туркменистан, никогда не завоевывал медалей на Олимпиаде.

У Эстонии и Латвии, до вхождения в СССР, было несколько медалей, но мы их естественно не учитываем.

А теперь от общей, перейдем к отдельным таблицам летних и зимних игр. (кликни)

Как обстоят дела по количеству медалей на зимних играх?

Источник

Топ 20 стран по золотым медалям на международных олимпиадах по математике, физике и химии

На этом видео показаны 20 ведущих стран мира с самым большим количеством золотых медалей Международной математической олимпиады (IMO) с 1959 года.

Международная математическая олимпиада (IMO) — это чемпионат мира по математике среди школьников, который проводится ежегодно в другой стране. Первая IMO была проведена в 1959 году в Румынии с участием 7 стран. Она постепенно расширилась до более чем 100 стран с 5 континентов.

На этом видео показаны 20 ведущих стран мира с самой большой суммой золотых медалей Международной олимпиады по физике (IPhO) с 1967 года.

Международная физическая олимпиада (IPhO) — это ежегодный физический конкурс для старшеклассников. Это одна из международных научных олимпиад. Первая IPhO была проведена в Варшаве, Польша, в 1967 году.

Каждая национальная делегация состоит не более чем из пяти студентов-конкурентов и двух лидеров, отобранных на национальном уровне. Наблюдатели могут также сопровождать национальную команду. Студенты соревнуются как личности, и должны сдавать интенсивные теоретические и лабораторные экзамены. За их усилия ученики могут быть награждены золотыми, серебряными или бронзовыми медалями или почетным упоминанием.

Теоретический экзамен длится 5 часов и состоит из трех вопросов. Обычно эти вопросы затрагивают более одной части. Практический экзамен может состоять из одного лабораторного обследования продолжительностью пять часов или двух, которые вместе занимают все пять часов.

На этом видео показаны 20 ведущих стран мира с самой большой суммой золотых медалей Международной химической олимпиады (МХО) с 1968 года.

Международная химическая олимпиада (МХО) — престижный международный химический конкурс для школьников старших классов. Первое МХО состоялось в 1968 году в Чехословакии. Он постепенно расширился до более чем 80 стран со всех континентов. Конкурс проводится каждый год, и организуется другой принимающей страной с соблюдением правил и традиций МХО.

Итого ТОП-10 по суммарному количеству золотых медалей на международных олимпиадах по математике, физике и химии будет выглядеть следующим образом:

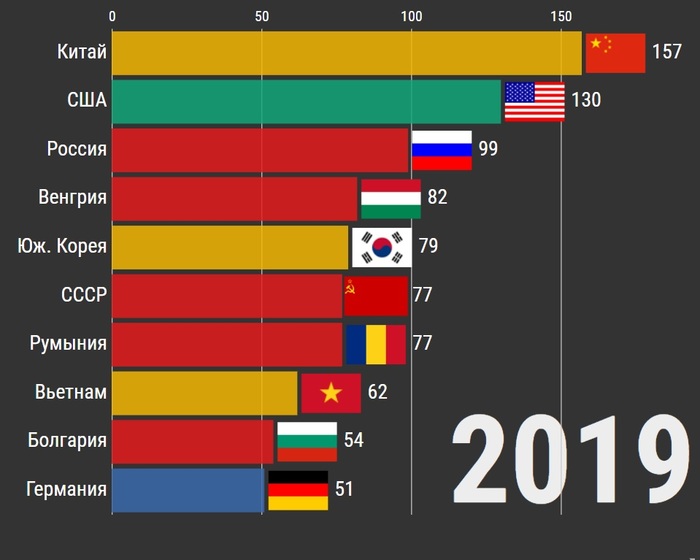
1. Китай — 384
2. Россия/СССР/СНГ — 374 (237/133/4)
3. США — 239
4. Южная Корея — 219
5. Тайвань — 164
6. Венгрия — 162
7. Румыния — 154
8. Германия — 123
9. Вьетнам — 120
10. Иран — 117

Золотые, Серебряные и Бронзовые медали добавляются, чтобы получить общее количество медалей. Это видео учитывает только летние Олимпийские игры.

Источник

Рейтинг лучших стран по медалям Чемпионатов Мира

Привет всем любителям футбиша! Чемпионаты мира — это настоящий праздник футбола для всего мира. Болельщики с каждого уголка планеты съезжаются для того, чтобы вместе лицезреть лучших футболистов, защищающих цвета своего национального флага. А какая же страна завоевывала медали ЧМ чаще остальных? Рейтинг учитывает золотые, серебряные и бронзовые медали. За 1 место начисляем 5 баллов , за 2 место 3 балла, за 3 место 1 балл.

5 место: Франция, 1 5 баллов

Французский футбол воспитал довольно большое количество сильных поколений, но не все из них добивались успеха на мундиалях. Например, Мишель Платини в качестве, наверное, лучшего футболиста с французским паспортом в истории на пике карьеры смог принести стране только одну бронзу в 1986 году .

Также одна бронза в 1958, серебро 2006 года и удаление Зидана. Больше всех для Франции сделал Дидье Дешам , выиграв ЧМ как игрок (капитан сборной) в 1998 и как тренер в 2018 году. Итого: 2 золота, 1 серебро, 2 бронзы

4 место: Аргентина, 19 баллов

Всего у альбиселесте 5 медалей на Чемпионатах мира. В 1978 году золото принесла команда во главе с Марио Кемпесом, который в финале забил дважды и отдал голевую передачу (3:1). Вторая победа пришлась на всеми известный ЧМ 1986 года в Мексике, где блистал Диего Марадона, практически в одно лицо затащивший аргентинскую сборную в финал . А его сольный проход на второй гол англичанам в 1/4 признали лучшим голом ХХ века.

Еще 3 раза сборная выигрывала серебро. Одно из них пришлось мундиаль 2014 года в Бразилии, где Лео Месси не хватило нападающих, чтобы не выпускать Игуаина на поле. Итого: 2 золота, 3 серебра

3 место: Италия, 27 баллов

Может быть, сейчас итальянский футбол переживает не лучшие времена, но в историческом масштабе эта нация одна из сильнейших в мире. Четырехкратные победители ЧМ брали золотые медали в 1934, 1938, 1982 и 2006 годах.

Как можно заметить, у Италии были сильные поколения сразу в нескольких временных промежутках, что в 30-е, что в 80-е, что в новейшей истории, скуадра адзурра показывали выдающийся футбол. Дважды они брали серебро, в 1970 и 1994 годах и одну бронзу в 1990-ом. Итого: 4 золота, 2 серебра, 1 бронза.

2 место: Бразилия, 33 балла

Хоть пентакампеоне и являются лучшей сборной по количеству побед на Чемпионатах мира (как вы поняли, их 5), если взглянуть на этот вопрос под углом общего количества призовых мест, то Пеле и компания с 1 местом этого рейтинга могут конкурировать только по золотым медалям. 1958, 1962, 1970, 1994 и 2002 года . Да, достижение очень, очень внушающее.

Если сейчас Бразилия считается фаворитом, но играет в не самый сильный футбол, то в те годы латиноамериканцы разрывали всех. «Мы забьем сколько захотим, а вы сколько сможете» — самая известная «стратегия» ХХ века. Также селесао по 2 раза брали серебряные и бронзовые медали. Итого: 5 золота, 2 серебра, 2 бронзы

1 место: Германия, 36 баллов

Немецкая машина имеет рекордное количество медалей на Чемпионатах мира — 12. Может, у Бразилии больше побед, но немцы чаще оказывались в призерах турнира, что также является неслабым достижением национального спорта. Золотых медалей же у Германии , а когда-то ФРГ, 4 — за 1954, 1974, 1990 и 2014 года. Занятно, что самое известное и трагичное событие в истории ЧМ связано именно с этими двумя сборными, те самые 7:1 на домашнем для Бразилии мундиале.

Также бундестим четырежды брали 2 место, и 4 раза третье. Итого: 4 золота, 4 серебра, 4 бронзы. Вот такой получился рейтинг. А как Вы считаете, что значит больше: рекорд Бразилии по победам или рекорд Германии по общему количеству медалей? Пишите в комментариях. Мне будет приятно, если вы поддержите канал лайком и подпиской. Увидимся! КАНАЛ ПРО ФУТБИШ

Источник

Топ-10 стран по золотым медалям на Международной математической олимпиаде (1959-2019)

На видео представлены топ-10 стран по количеству золотых медалистов Международной олимпиады по математике с 1959 года по 2019 год.

По состоянию на 2019 год по золотым медалям СССР до сих пор входит в 10-ку. Россия, набрав 99 золотых медалей, вышла на третье место.

Из других республик бывшего Советского Союза наиболее успешно выступает команда Украины (39 золотых медалей).

Ниже представлены результаты республик, входивших в состав Советского Союза:

Россия — 99 (золотых медалей)

Стоит отметить, что в 1992 году объединенная команда СНГ завоевала 2 золотые медали.

Дубликаты не найдены

Лига математиков

334 поста 1.6K подписчиков

В итоге в 21м веке СССР упустил своё преимущество. Китай уже не догонишь.

В этом и проблема — всё время стараемся кого то догнать, перегнать, зачастую вопреки здравому смыслу.

Конкретно тут смысл в развитии математики в школах.

Китайцы и за себя и США топят

Половину полосочки США можно смело плюсовать к Китаю

Вот их типичная сборная

Есть шутка, что это вторая сборная Китая. Или не шутка.

А где Индия. У них вроде бы программистов много, или они в олимпиады не пчень?

Так ты выбирай за кого голосовать, если голосуешь за тех кто ворует и денег на обучение не остается, то чему удивляться?

Ответ на пост «В России резко растет эмиграция ученых»

Ок, а теперь взглянем на этот вопрос с другой стороны.

Итак, по таблице госстата о выпускниках 2017-2019 годов, 61% из них учились на юристов, управленцев, спортсменов, психологов и прочих ландшафтных архитекторов и литературоведов. (архив за 2020 год)

По данным Минобра, их еще больше — 64%.

Таким образом, только треть наших студентов получают какое-то реальное образование, которое позволяет на самом деле если не двигать, то хотя бы поддерживать в работоспособном состоянии научно-технический потенциал страны, включая сюда лечение людей, сельское хозяйство и легкую промышленность как витально критичные. Ну ок, прибавим сюда педагогов — будет чуть больше трети. Количественно это около 600 тыс., причем какая-то их часть. процентов 20-25, в итоге по специальности работать не будет.

Это ничтожно мало.

Ситуация с уровнем науки в нашей стране конечно ужасная, это факт. Но она в конце концов говорит скорее о дальних перспективах. А вот нехватка грамотных инженеров, врачей, энергетиков и агрономов может нам аукнуться уже лет через 20-30 самым натуральным апокалипсисом. Мы тут не в Оклахомщине, у нас без инженерных сетей и агротехнологий будет тупо холод и голод.

Я тоже считаю, что науке надо много денег и мало бюрократии. Но сегодня критичнее все-таки более приземленные потребности общества, и вот то, что и на них забивают власти, мне кажется признаком намного более угрожающим.

В России резко растет эмиграция ученых

С 2012 года в 5 раз (с 14 до 70 тысяч человек) увеличилось количество ученых и высококвалифицированных специалистов, уезжающих из России, — сообщил главный ученый секретарь РАН Н.Долгушкин. По его словам, только за последние три года число ученых в стране сократилось на 30 тыс. В итоге Россия не может выполнить показатели нацпроекта «Наука», который ставил задачу увеличить число специалистов за три года на 35 тыс. человек

Сейчас Россия — единственная из развитых стран, где несколько десятилетий подряд сокращается число ученых. В 1990 году Россия занимала первое место в мире по числу ученых, но с тех пор их количество снизилось с 992 тыс. до 348 тыс. Еще три года назад РФ находилась на 4 месте в мире по количеству исследователей. Сегодня она находится на шестом — уточнил академик.

Как считает академик Долгушкин, есть три главных риска для российской науки: недостаток финансирования, отсталая инфраструктура и самый главный — «кадровый, интеллектуальный потенциал».

Что такое расстояние и когда Пи = 4 ?

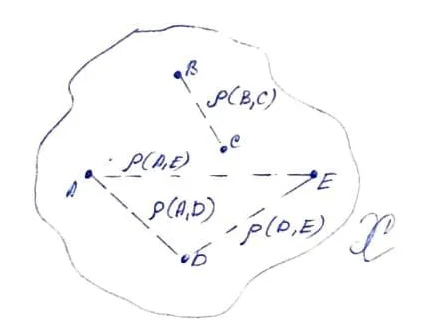
Задумывались ли Вы когда-нибудь о том, что такое расстояние ? Какими свойствами должна вообще обладать некая величина, чтобы носить такое гордое наименование? Сегодня я расскажу Вам, что понимается под «расстоянием» в математике.

Итак, начнём с рисунка. Вам, конечно, известно, что основой всей математики является теория множеств, ведь из неё можно вывести практически все термины, которыми оперирует царица наук. Расстояние — не исключение. Расставим на бумаге в произвольном порядке элементы произвольного множества X = :

Каждым двум точкам из этого множества сопоставим некое отношение (или величину) , которую обозначим греческой буквой ρ. Пара (X, ρ) — в математике называется пространством, а от характера ρ зависит то, каким оно будет. Например, если ρ носит характер метрики, то пространство будет называться метрическим. Но что же такое метрика?

Чтобы назвать отношение ρ метрикой необходимо выполнить три условия, которые называются аксиомами метрического пространства:

Предпоследняя строчка определяет метрику как отображение декартова произведения элементов множества в вещественную ось. Третье условие называется неравенством треугольника, известным всем еще со школьной скамьи. Все аксиомы наглядно показаны на первом рисунке.

Обратите внимание на тонкость: само отношение называется метрикой, а вот результат применения этого отношения (читай, отображение) к двум точкам метрического пространства — расстоянием.

Таким образом, только в пространствах, наделенных метрикой, имеет смысл говорить о расстоянии.

Какие бывают метрики ?

В целом, любое отношение, удовлетворяющее вышеперечисленным аксиомам, имеет право называться метрикой. Самый простой способ задать метрику — это посмотреть на числовую ось:

Все аксиомы легко проверяются:

ρ(A,C) ≤ ρ(A,B) + ρ(B,C) — выполняется в форме равенства.

Таким образом, разница между вещественными числами — суть расстояние, а (R, ρ) — метрическое пространство.

Странно говорить о пространстве на прямой, не так ли? Если смущает, приглашаю на знакомую всем координатную плоскость. Отметим на ней два элемента (точками они, формально, станут после доказательства метризуемости), каждому из которых поставим в соответствие упорядоченную пару (x,y):

Аксиомы метрики для введенного нами соотношения также доказываются. Единственное, что неравенство треугольника уже выполняется в классическом виде, данном миру еще Евклидом.

В математике такое называют метрическим пространством R². Расстояние в нём — это фактически длина гипотенузы прямоугольного треугольника, вычислимая по теореме Пифагора. Множество точек, равноудаленных от данной, является окружностью, а число π ≈ 3,14.

Без потери общности можно сопоставить каждому элементу уже тройку координат, что приведет нас к привычному метрическому пространству R³. Окружность в нём, например, станет сферой.

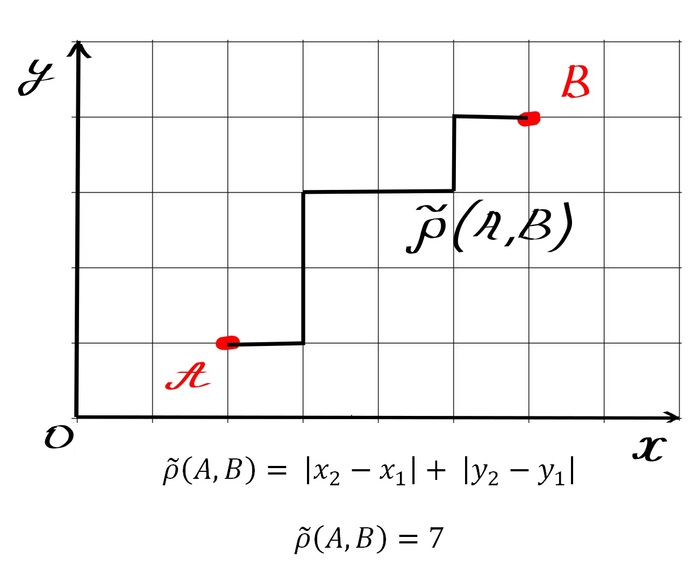
А теперь давайте определим метрику таким образом, как будто мы не можем перемещаться в пустоте между клеток, а только по линиям координатной сетки:

Для такой метрики, как и для привычной нам евклидовой, все аксиомы выполняются. Пространство с такой метрикой называется манхэттеновским, потому что правила игры в нём очень сильно напоминают передвижение по прямоугольной сетке городских кварталов.

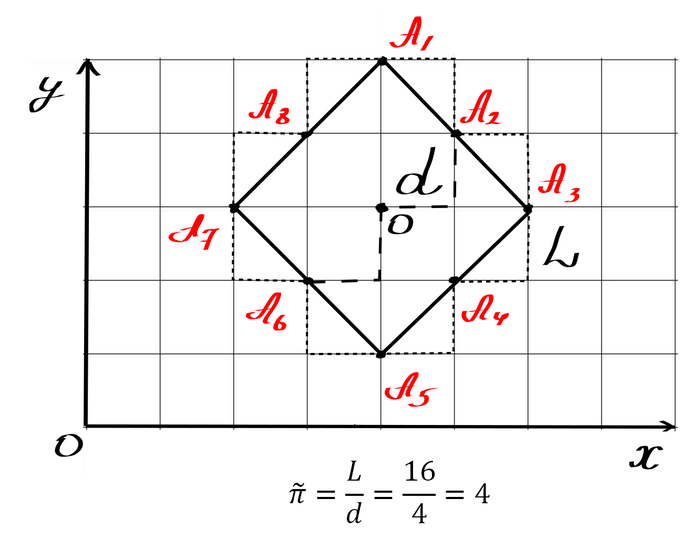
Кстати, в качестве заключения. Окружность – это геометрическое место точек. равноудаленных от данной точки, которая называется центром окружности. Число π – отношение длины окружности к диаметру. Смотрим дальше:

Да, только что я показал Вам, что число π может быть равно 4.

Больше интересной математики в телеграмм — «Математика не для всех»

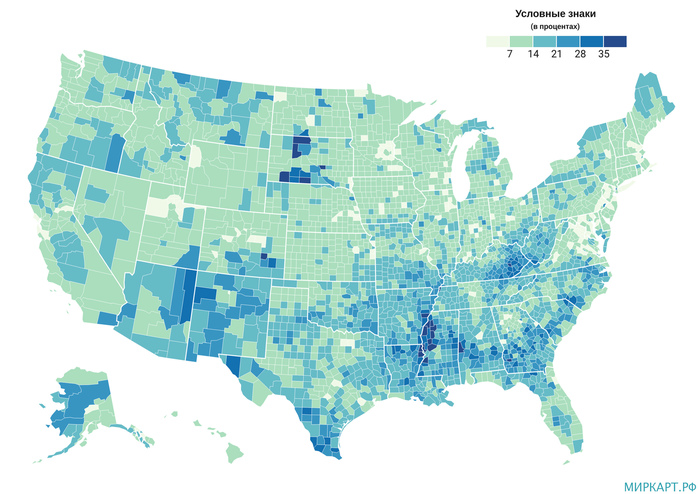
Подборка интересных географических карт №5

Порог бедности в Соединенных Штатах вычисляется на основе множества различных индикаторов и отличается в зависимости от величины домохозяйства, а также возраста его членов. Например, по данным Бюро переписи населения США в 2019 году для одного человека он составлял 13011 долл. США, а для семьи из трех человек (с одним ребенком) этот порог был равен 20578 долл. США. Около 12.3% жителей страны считались бедными на 2019 год. По штатам наибольший уровень бедности отмечался в Миссисипи — 19.5%, а наименьший в Нью-Гемпшире — 7.5%.

По округам разрыв еще больше, ниже представлен перечень округов с наибольшей долей бедного населения:

— Зибах (Ziebach County), Южная Дакота — 47,7%;

— Тодд (Todd County), Южная Дакота — 43,4%;

— Мэдисон Пэриш (Madison Parish), Луизиана — 41,1%;

— Корсон (Corson County), Южная Дакота — 40,3%;

— Оглала-Лакота (Oglala Lakota County), Южная Дакота — 40,1%;

— Кроули (Crowley County), Колорадо — 40,0%;

— Баффало (Buffalo County), Южная Дакота — 39,8%.

А наименьшая доля бедного населения была характерна для округов:

— Линкольн (Lincoln County), Южная Дакота — 3,8%;

— Лос-Аламос (Los Alamos County), Нью-Мексико — 3,5%;

— Фолс-Черч (Falls Church city), Вирджиния — 3,5%;

— Лаудон (Loudoun County), Вирджиния — 3,1%;

— Дуглас (Douglas County), Колорадо — 2,7%.

Источник данных: Служба экономических исследований Министерства сельского хозяйства США

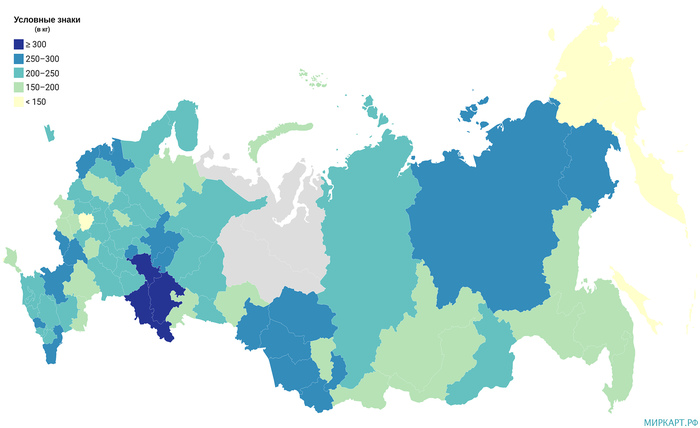
Потребление молока и молочных продуктов на душу населения по регионам России в 2019 году

Потребление молока и молочных продуктов в России* на душу населения по итогам 2019 года составило 234 кг, что несколько ниже уровня 2010 года, когда оно было равно 245 кг. По регионам существуют большие различия в значении этого показателя, например, в лидерах Республика Татарстан — 359 кг, Оренбургская область и Республика Башкортостан — по 301 кг, Санкт-Петербург — 297 кг, Кабардино-Балкарская Республика — 285 кг. А минимальный уровень потребления отмечен для Чукотского АО — 106 кг, Тульской области — 129 кг, Севастополя — 141 кг, Сахалинской области — 144 кг, Камчатского края — 145 кг.

*Данные по автономным округам, входящим в состав областей, не разрабатывались в связи с отсутствием информационной базы.

Источник данных: Росстат

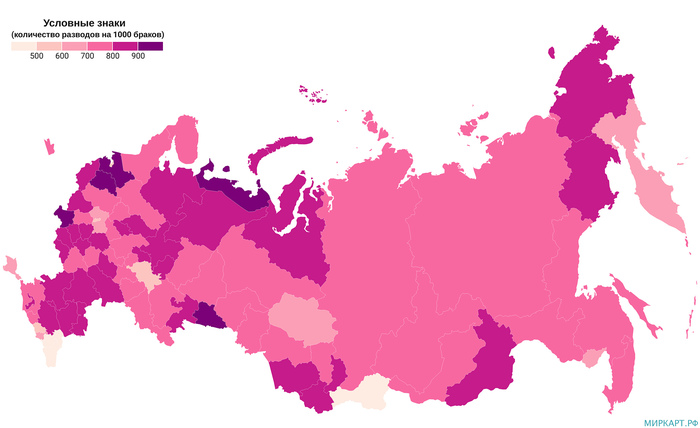
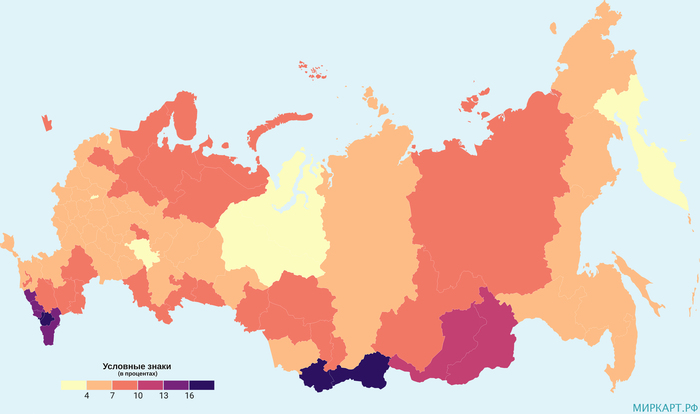
Число разводов на 1000 браков в России по регионам на 2020 год

В 2020 году в большинстве регионов России увеличилось количество разводов на 1000 браков. Если в 2019 году этот показатель в стране был равен 653, то в 2020 году он увеличился до 732 (+12,1%). Т. к. это средний показатель, то, соответственно, в ряде регионов это значение еще выше, например, Ненецкий АО — 994, Ленинградская область — 968, Курганская область — 918, Новгородская область — 914. На 2019 год только в 4 регионах количество разводов на 1000 браков превышало 800, а в 2020 году их число увеличилось до 36 регионов.

Ряд субъектов выделяются большим процентным ростом показателя, например, Белгородская область, где он составил 34.5% (с 631 до 849), Республика Ингушетия — 32% (с 205 до 271), Брянская область — 31% (с 697 до 913) и т. д.

Уменьшилось число разводов на 1000 браков только в 7 регионах страны, среди которых Еврейская автономная область (-13.42%), Сахалинская область (-7.45%), Камчатский край (-7.05%), Томская область (-3.01%), Ленинградская область (-1.2%), Амурская область (-0,94%), Мурманская область (-0.15%).

Источник данных: Росстат

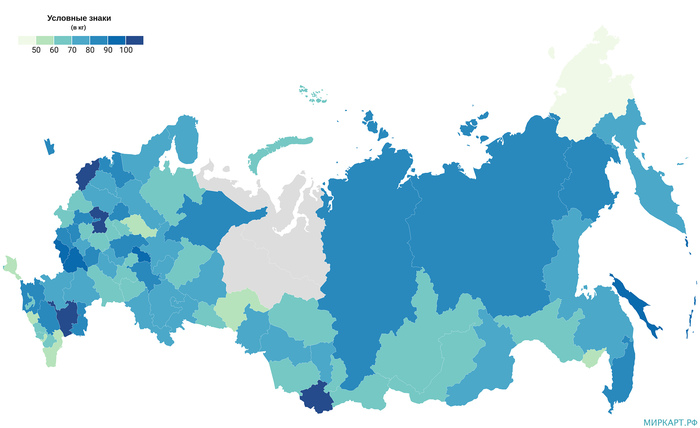
Потребление мяса и мясопродуктов на душу населения по регионам России в 2019 году

Среднее потребление мяса и мясопродуктов (включая субпродукты II категории и жир-сырец) на душу населения в России* по итогам 2019 года составило 76 кг, при этом в 33 регионах значение показателя было выше, в 3 регионах оказалось равным, а в 46 регионах ниже среднего российского уровня. Лидерами по потреблению продуктов этой категории являлись Республика Калмыкия — 116 кг, Московская область — 106 кг, Псковская область — 104 кг, Республика Алтай — 101 кг, Белгородская область — 96 кг. Последние места в списке регионов по данному показателю заняли Чукотский АО — 44 кг, Республика Дагестан — 51 кг, Еврейская автономная область — 53 кг, Тюменская область — 54 кг, Республика Крым — 55 кг.

*Данные по автономным округам, входящим в состав областей, не разрабатывались в связи с отсутствием информационной базы.

Источник данных: Росстат

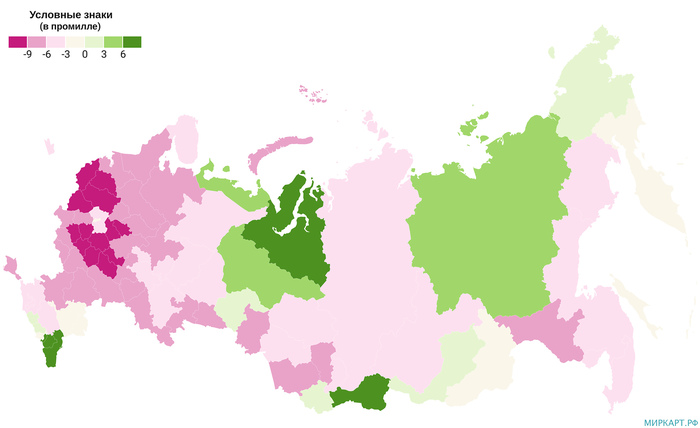
Коэффициент естественного прироста по регионам России в 2020 году

Коэффициент естественного прироста – разность общих коэффициентов рождаемости и смертности. Исчисляется в промилле (на 1000 населения).

По оперативным данным Росстата в 2020 году в России было только 13 регионов с положительным естественным приростом населения, а также один регион (Тюменская область), где данный показатель был равен нулю. Среднее значение коэффициента по стране составило -4.7. Общее число родившихся в 2020 году равно 1435,8 тыс. чел., а умерших — 2124,5 тыс. чел., т. е. наблюдалась естественная убыль в размере 688.7 тыс. чел. При этом количество жителей страны за год сократилось на 510 тыс. чел., что дало 146.238 млн чел. населения на 1 января 2021 года, т. е. часть естественной убыли компенсировалась миграцией.

Первая 5-ка регионов по коэффициенту естественного прироста:

— Чеченская Республика — 14,0;

— Республика Ингушетия — 12,9;

— Республика Тыва — 10,8;

— Республика Дагестан — 8,7;

— Ямало-Hенецкий АО — 7,0.

Последние места в стране по величине показателя занимали:

— Тамбовская область — -10,4;

— Тверская область — -10,4;

— Владимирская область — -10,7;

— Псковская область — -10,9;

— Тульская область — -11,3.

Источник данных: Росстат

Самая красивая формула математики. Пришло время узнать, как её вывел Эйлер

Одна из самых первых статей на моём канале была посвящена самому красивому математическому тождеству, которое выводится на основе великолепной формулы Эйлера.

Тогда я только констатировал факт безмерного восхищения, но никаких доказательств не привел. Пришло время исправить этот недостаток. К тому же, сам вывод так же изящен и требует знания только школьной математики. Поехали!

Ну ладно, чуть больше, чем школьных. Для вывода требуется понимание, что большинство знакомых в школьном курсе математики функций можно разложить в ряд Маклорена.

Для этого, всего лишь, требуется уметь вычислять производные и подставлять «0» вместо х. Возьмем экспоненциальную функцию:

Производная от экспоненты равна ей самой, e^0 = 1 в каждом из слагаемых бесконечного ряда. Подставим x=1, получим e^1=e = 1 + 1 + 1/2 +1/6 + 1/24 + . ≈ 2,71828.

Главное не запутаться с чередованиями знаков при возведении мнимой единицы в различные степени.

Для cos(x): cos'(x) = -sin(x), cos»(x) = -cos(x), cos»'(x) = sin(x), cos»»(x) = cos (x) — круг замкнулся на 4 шаге. Дальше опять аккуратно со знаками.

Последнее тождество по результатам самых разных голосований, опросов и является самой красивой математической формулой, которую только придумал человек. Не красотой едины: сама формула Эйлера (в символьном виде) — одно из важнейших выражений, связывающее мир комплексных и вещественных чисел, экспоненту и тригонометрию.

Экспоненциальное представление комплексных чисел удобнее чем алгебраическое и используется в обработке сигналов, электротехнике, картографии, квантовой механике и в многих других областях науки.

Больше интересной математики в телеграмм — «Математика не для всех»

Депутаты Госдумы в окончательном чтении одобрили законопроект о просветительской деятельности

За проголосовали 308 депутатов, против — 95, воздержался от голосования один депутат. После того, как закон примет Совфед и подпишет президент, любую образовательную деятельность вне школ и университетов нужно будет согласовывать с государством.

Гениальная формула Виета, которую не проходили в школе

Приветствую Вас, уважаемые Читатели! Решение кубических уравнений со школы вызывало определенные сложности. Мало того, что среди корней таких уравнений часто встречаются числа с мнимой частью, так и формула Кардано для решения таких уравнений достаточно сложная и мудрёная.

Остается еще вариант разложить кубический многочлен на множители, использовать теорему Безу для подбора целых корней, но и это не всегда получается. Сегодня я хочу рассказать о тригонометрическом способе решения кубических уравнений, который разработал наш старый знакомый Франсуа Виет.

Добрый, усатый, твой — Франсуа Виет

Тригонометрическая формула Виета хоть и выводится достаточно просто, однако всё так же содержит громоздкие итоговые формулы. Чаще всего таким методом решения пользуются, чтобы получить приближенное значение корней уравнения, что достаточно для практических расчетов, итак:

В первую очередь вычисляются величины Q, R и S, от которых зависит, сколько и каких корней будет иметь уравнение (в нём а=1, b=-2, c=-1) . В нашем случае S>0, а значит шайтан-уравнение имеет три вещественных корня:

Вот такие формулы для корней этого уравнения. Если Вы думаете, что они сложные, то глубоко ошибаетесь. При других S в формулах появляются даже гиперболические арк-функции!

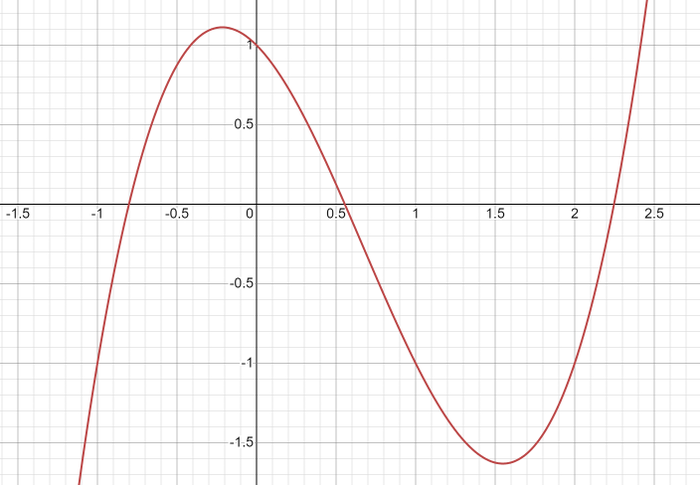
Получить здесь красивые числа для вычислений — большая удача, но с помощью калькулятора найти решение просто. Проверим на графике

А вот и график нашей функции. Нули совпадают с найденными нами по тригонометрической формуле Виета

Самое большое достоинство метода — это возможность запрограммировать алгоритм решения любого кубического уравнения со сколь угодно нужной степенью точности. Недаром, многие из представленных в интернете онлайн-калькуляторов решают кубические уравнения именно с помощью тригонометрической формулы Виета.

Больше интересной математики в телеграмм — «Математика не для всех»

Красивый способ найти все простые числа. Почему про него молчит Википедия?

Самым известным для способом получения простых чисел является «решето Эратосфена». Сегодня я подготовил для Вас значительно менее известный, но поистине великолепный способ, который принадлежит перу ныне здравствующего Юрия Владимировича Матиясевича — советского и российского академика, перечисление регалий которого займет несколько страниц.

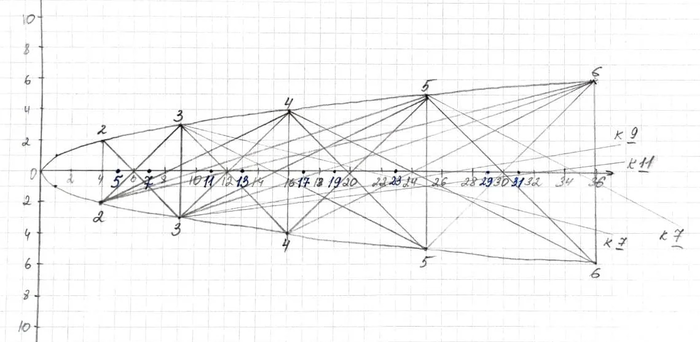
Способ нахождения простых чисел — чисто геометрический. На первом чертеже я покажу и опишу конечный результат, а на втором и третьем покажу простое доказательство, которое поймет любой школьник:

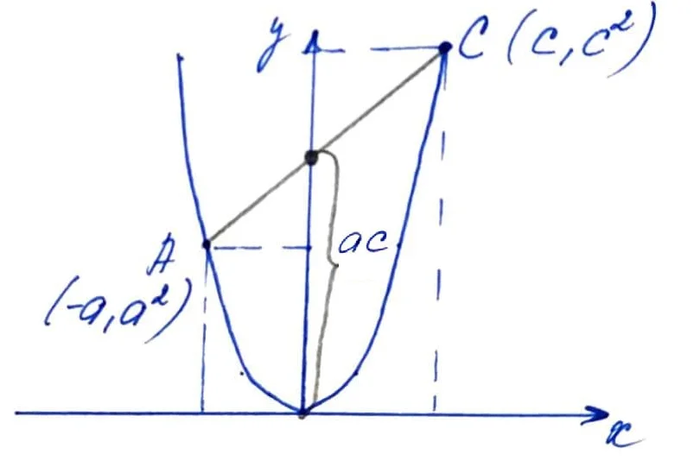
Начертим обычную параболу y=x^2. Не обращайте внимания, что и сверху и снизу числа положительные, это неважно в данном случае. Соединим каждую точку на ветви сверху со всеми точками на нижней ветви. Оказывается, что точки, в которых эти линии никогда не пересекут горизонтальную ось соответствуют простым числам — 5,7,11,13,17,19 и т.д. Такой способ и называется решетом Матиясевича-Стечкина.

Формализуем нашу задачу. Обозначим координаты точек на разных ветвях параболы буквами а и с. Чтобы доказать, что расстояние на рисунке равно ас, необходимо построить уравнение прямой, проходящей через две точки (привет, 7 класс!) и в нём положить х=0

Это мы делаем легко и непринужденно. Получается, что любой отрезок, соединяющий две точки А и С, лежащие на противоположных ветвях параболы, пересекает ось у в точке с координатой (0, ас):

Тут и открывается загадка «просеивания» простых чисел, ведь они не являются произведением никаких двух чисел, кроме себя и единицы. Как Вам способ? По-моему, очень красивый, а между тем, про него даже отсутствует страница в Википедии! Спасибо за внимание!

Больше интересной математики в телеграмм — «Математика не для всех»

Подборка интересных географических карт №4

Уровень безработицы населения в возрасте 15 лет и старше по регионам России в сентябре-ноябре 2020 года

Уровень безработицы — отношение численности безработных определенной возрастной группы к численности рабочей силы (занятых и безработных) соответствующей возрастной группы, рассчитанное в процентах.

Статистика по уровню безработицы населения в возрасте 15 лет и старше по субъектам Российской Федерации была собрана по данным выборочных обследований рабочей силы Росстатом. Среднее значение данного экономического показателя за сентябрь-ноябрь 2020 года в стране составило 6.2%, что выше уровня соответствующего периода 2019 года, когда безработица составила 4.6%.

Первые пять регионов страны с самой высокой долей безработных в рассмотренный период:

— Республика Ингушетия — 31,0%;

— Чеченская Республика — 22,3%;

— Республика Тыва — 19,9%;

— Республика Алтай — 16,3%;

— Кабардино-Балкарская Республика — 15,6%;

Регионы с самым низким уровнем безработицы:

— Республика Татарстан — 3,8%;

— Камчатский край — 3,7%;

— Ханты-Мансийский автономный округ — Югра — 3,3%;

— Ямало-Ненецкий автономный округ — 2,6%.

Источник данных: Росстат

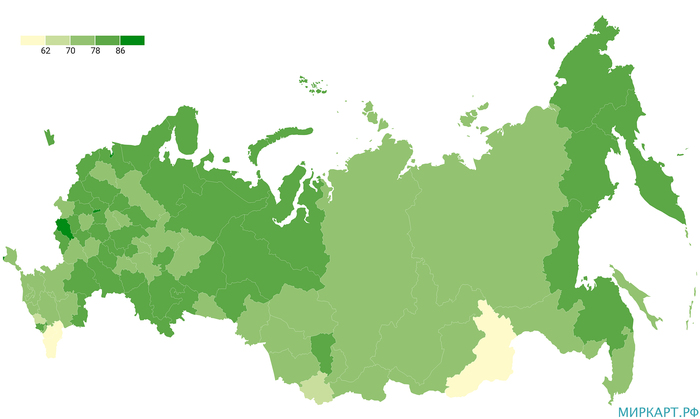
Доля рабочей силы в возрасте 22 лет и старше, имеющей среднее профессиональное и высшее образование, в общей численности рабочей силы соответствующего возраста

В 2019 году, по данным выборочных обследований рабочей силы, в России доля рабочей силы в возрасте 22 лет и старше, имеющей среднее профессиональное и высшее образование, в общей численности рабочей силы соответствующего возраста составляла 79.2%. По регионам страны наибольшим этот показатель был в Москве — 94%, Севастополе — 87.5%, Санкт-Петербурге — 86.7%.

К субъектам РФ, где была зафиксирована наименьшая доля людей рассматриваемой категории, относились: Чеченская Республика — 54%, Республика Дагестан — 55.2%, Забайкальский край — 61.8%.

Источник данных: Росстат

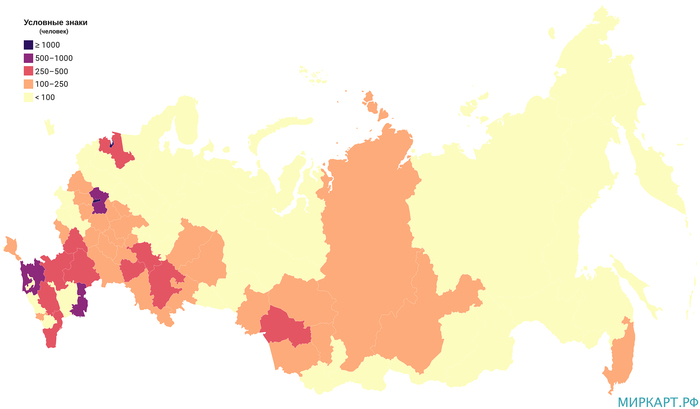
Численность населения в возрасте 100 лет и более по регионам России на январь 2020 года

Количество жителей России в возрасте 100 лет и более с января 2010 г. по январь 2020 г. увеличилось с 7667 человек до 22898 человек, т. е. рост составил почти 200%. Единственным регионом России, где в январе 2020 года не было жителей в этой возрастной категории, стал Чукотский автономный округ. Самое большое количество жителей в возрасте 100 лет и более в Москве — 7684 чел. и в Санкт-Петербурге — 3467 чел. Это значит, что на эти два региона приходится почти половина общероссийского значения данного показателя. У следующей за ними Астраханской области было только 752 чел. в этой возрастной категории.

Источник данных: Росстат

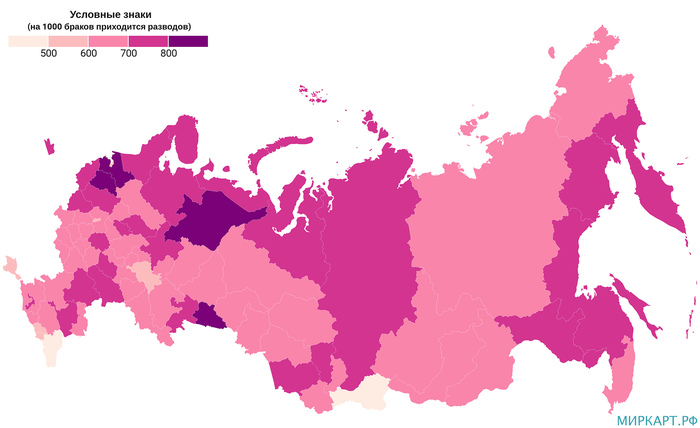
Соотношение браков и разводов по регионам России в 2019 году

В 2019 году на каждые 1000 браков в России приходилось 653 развода, что на 127 больше уровня 2010 года, т. е. рост этого показателя за данный период составил 24.1%. При этом в 62 регионах страны значение было выше общероссийского. В РФ всего 4 региона, где на 1000 браков приходилось бы менее 500 разводов: Чеченская Республика — 157, Республика Ингушетия — 205, Республика Дагестан — 332, Республика Тыва — 341. В лидерах же, по итогам 2019 года, находились Ленинградская область — 980, Курганская область — 815, Республика Коми — 803, Новгородская область — 802.

Если не брать в расчет Севастополь и Республику Крым, по которым у Росстата не было информации на 2010 год, то среди оставшихся 83 регионов страны только один продемонстрировал снижение показателя в 2019 году по сравнению с 2010 годом. Им стал Чукотский АО, где в 2010 году на 1000 браков пришлось 753 развода, а в 2019 году 686, т. е. на 8.9% меньше. Хотя тут нужно учитывать, что в этом регионе проживает около 50 тысяч человек, что значит сравнительную легкость колебаний многих индикаторов.

Регионами — лидерами по росту показателя стали Республика Ингушетия — на 79.8%, Республика Дагестан — на 74.7%, Чеченская Республика — 68.8%. Т. е. те субъекты РФ, в которых в 2019 году было меньше всего разводов в расчете на 1000 браков, являются также регионами, где по сравнению с 2010 годом произошел наибольший рост этого показателя.

Источник данных: Росстат

Число погибших в дорожно-транспортных происшествиях в России на 2019 год по регионам

В методических пояснениях Росстата указано, что погибшим в результате ДТП считается лицо, погибшее на месте ДТП, либо умершее после ДТП в течение 30 последующих суток. Дороги России постепенно становятся более безопасными, в 2005 году в нашей стране в дорожно-транспортных происшествиях погибали 23.7 чел. на 100 000 населения, в 2010 году это значение уменьшилось до 18.6 чел., а по итогам 2019 года составило 11.6 чел., т. е. около 17 тыс. чел. Получается, что смертность в ДТП в период 2010-2019 гг. снизилась на 37.6%. Показатель уменьшился не только на уровне страны в целом, но и во всех регионах*. Следует отметить, что число самих дорожно-транспортных происшествий уменьшилось только на 19.8%: со 139.6 на 100 000 населения до 112, т. е. около 164 тыс. ДТП на 2019 год.

Первая 5-ка регионов по количеству погибших в ДТП на 100 000 населения в 2019 году:

1. Республика Тыва — 31,9;

2. Республика Калмыкия — 29,4;

3. Забайкальский край — 22,8;

4. Рязанская область — 21,5;

5. Ленинградская область — 20,7;

И 5-ка регионов с наименьшими значениями данного показателя:

81. Ненецкий автономный округ — 4,5;

82. Санкт-Петербург — 4,2;

83. Севастополь — 4;

85. Чукотский автономный округ — 2;

*Данные по Республике Крым и г. Севастополь у Росстата за 2010 год отсутствуют, т. к. на тот момент эти регионы не отображались в отечественной статистике.

Источник данных: Росстат

Красивейший интеграл Эрмита, который переворачивает школьную математику. Факториал дробного числа.

Приветствую Вас, уважаемые Читатели! Сегодня достаточно сложный материал, особенно для тех, кто давненько не сталкивался с интегралами. Впрочем, я постараюсь настолько, насколько это возможно, показать Вам совершенно удивительную дорожку к натуральным числам, проявляющуюся в хитросплетениях бесконечности, интеграла и числа Эйлера. Позвольте представить, интеграл Эрмита:

В данном интеграле k — это некое число, и что-то подсказывает, что результат вычисления этого интеграла будет с ним связан (да еще как. ). Чтобы вычислить такой интеграл необходимо применить формулу интегрирования по частям:

Очень важным моментом будет выбор переменных. Сделаем его таким образом, чтобы при взятии производной показатель степени k уменьшился. Смотрите (забыл дописать dx в первой строчке):

Таким образом наш интеграл разбивается на два слагаемых. Давайте разберемся с первым: для этого нам понадобится просто подставить вместо x пределы интегрирования:

Мы применили k раз правило Лопиталя для раскрытия неопределенности бесконечность/бесконечность

Первое слагаемое, как стало понятно, равно 0. Что делать со вторым? Ключевая идея в том, чтобы продолжать интегрирование по частям. Функция имеет похожий вид на исходную, значит порождаемые её первые слагаемые вида u*v всегда будут равны 0.

Второе же слагаемое при интегрировании k раз вырождается в произведение факториала числа K и еще одного интеграла, теперь уже табличного:

Вы понимаете, страшный интеграл, в котором и намека нет на «красивый» целый ответ вообще оказывается равным натуральному числу! Однако, тот самый шокирующий вывод, переворачивающий школьную математику, произойдет, если мы вспомним, что интеграл — это площадь ограниченная кривой (в данном случае x^k*e^(-x)) и пределов интегрирования (от 0 до бесконечности).

Так что же нам мешает взять k не целым числом, а, например, рациональным. А ничего, ведь площадь под графиком — она и в Африке площадь, а, значит, мы только что получили расширение понятия факториала на все числа, в т.ч. комплексные и подобрались к одному из ключевых понятий математического анализа — гамма-функции.

Кроме того, этот интеграл используется в крайне красивом доказательстве трансцендентности числа Эйлера, о котором я расскажу позже, если Вам нравятся такие материалы. Спасибо за внимание!

Больше интересной математики в телеграмм — «Математика не для всех»

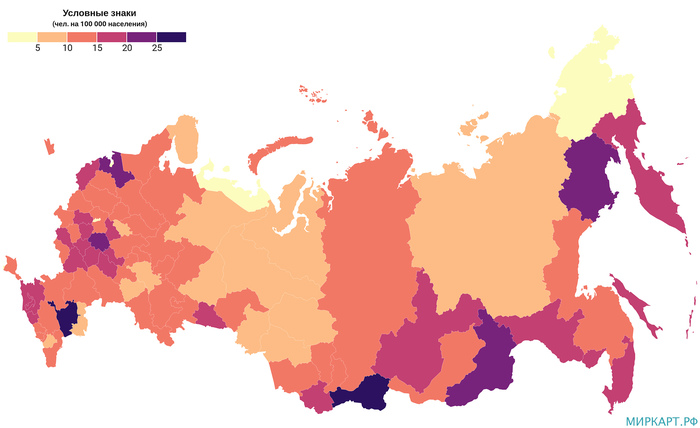
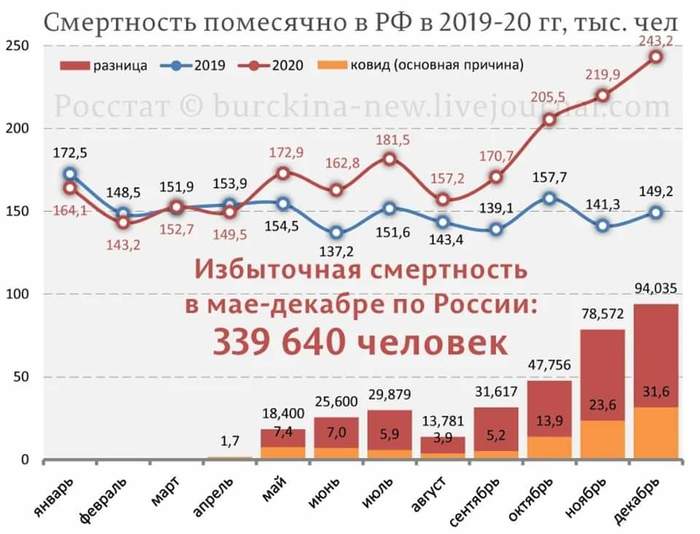
Смертность помесячно в РФ в 2019-20

Немного статистики к посту «Особенности состава разыскиваемых преступников из РФ по данным Интерпола»

Посмотрев на пост Особенности состава разыскиваемых преступников из РФ по данным Интерпола, стало интересно взглянуть на закономерность через цифры и на всей картине в целом (сайт при поиске показывает лишь до 160 человек за раз). Заодно проверить, нет ли искажения восприятия.

В общем, вытянул сведения по всем 2869 лицам. Смотрим:

Кому интересно покрутить данные, вот таблица:

Куда а уходят кадры

Вузы постоянно жалуются, что нет притока молодой крови. А вы думаете, кто-то в академической среде людей удерживает? Не то, что не удерживает, нас (молодежь) ещё и стараются выгнать побыстрее, если ты, конечно, не блатной безрукий профессорский сынок/внучок.

Давным-давно я работала в одном уральском университете. Когда я только пришла на кафедру, средний возраст преподавателя по этой кафедре составлял 67 лет. В основном, конечно, преобладал контингент за 70. Но было и несколько перспективных сотрудников до 30: 3 доцента (два из которых работали по совместительству) и 3 инженера. Ну и я, вот, только пришла (ещё не было 25).

Так вот. В 2012 (возможно, в 2011 — точно не помню) Министерство образования выпустило приказ (или закон, или подзаконный акт, или ФЗ, короче, хз), согласно которому необходимо было нормировать штат по количеству студентов. В общем, всех подробностей уже не упоминить, но всё сводилось к сокращению штата. И как вы думаете, кого уволил заведующий? 75-летних бабок? Нет. Он уволил молодежь. Из троих молодых доцентов остался один, и тот перевёлся на половину оклада. Из троих инженеров уволил всех: один ушел преподавателем в другой ВУЗ, второй перевёлся на другой факультет, а третий уехал в Москву. Кстати, третий сказал тогда: «Ну и хорошо, так и надо, а то я бы ещё тут не пойми на сколько завис. Эта работа как свинью стричь: визга много, а шерсти ноль». У него на тот момент были хорошие перспективы. Через год-два стал техническим директором какого-то околометаллургического предприятия.

К слову, меня тогда тоже ссаной тряпкой погнали. Но у меня аспирантура была, и поэтому я ещё какое-то время проторчала, пока окончательно не выперли.

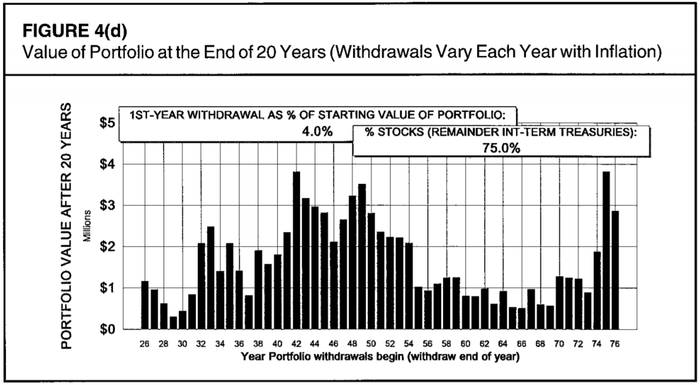
Правило 4% — о чём вам не расскажет Пенсионный фонд России

Правило 4% очень распространено на западе в контексте пенсионных сбережений и планировании жизни на пенсию. Человек всю жизнь накапливает себе капитал на пенсию. Делает он это на специальных пенсионных счетах, кто-то — в коллаборации с работодателем, кто-то — самостоятельно. Чаще всего пенсионные сбережения хранятся в ценных бумагах — акциях и облигациях.

Как устроена наша пенсионная система, и как она относится к тому, что будет описано в этом посте — об этом в самом конце.

Правило 4% предполагает снятие 4% от капитала в первый год и снятие суммы, равной предыдущей, но с поправкой на инфляцию — в последующие годы.

Обычно статьи с описанием этого правила гласят: если снимать средства из пенсионного портфеля по Правилу 4%, то ваши сбережения в ценных бумагах практически при любом развитии событий не будут “худеть”.

Но кто придумал это правило? Как оно работает с точки зрения математики? Подходит ли оно для всех типов портфелей? Давайте разбираться.

Это правило сформулировал не какой-то видный учёный-экономист, а практик — обычный независимый пенсионный советник Уильям Бенген в октябре 1994 года, оригинал статьи здесь.

Вот что он написал тогда, в 1994 году:

Заглянем в будущее, 2004 год. Вы — управляющий пенсионного фонда, и вы сделали достойную работу показав хорошую доходность за 10 лет. Ваши клиенты довольны. Рынки были щедрыми, они пузырились вовсю, и ваши клиенты вышли на пенсию с жирными счетами, а вы посоветовали им фиксированную ежегодную сумму снятия с поправкой на среднюю инфляцию. Суммы более чем хватает на достойную пенсию, клиенты вам благодарны.
2006 год. Рынки падают на 35% за последние 2 года, худшее время после рецессии 1973-1974 гг. ФРС врубила печатный станок. Многие из ваших клиентов обеспокоены тем, что им придется сократить свои траты чтобы сохранить капитал при выходе на пенсию. Вы успокаиваете их, напоминая им,что вы тщательно рассчитали их показатели на исторических данных. Но вы не можете избавиться от угрызений совести, что вы что-то рассчитали не так.
2009 год. Как вы и прогнозировали,фондовый рынок хорошо восстановился за последние три года, и все клиенты вернулись к сумме, которая была вначале, несмотря на фиксированные снятия для жизни на пенсии. Однако у ваших клиентов есть новая жалоба: они не могут продолжить жить на эту сумму. ФРС разогнала инфляцию! Инфляция составила аж 8% в год на протяжении 5 лет. Качество жизни для пенсионеров с фиксированной выплатой снизилось значительно. Вы не можете повысить выплату, ведь тогда ваши расчеты пойдут коту под хвост, и есть немалая вероятность того, что при индексации выплат на уровень этой инфляции, пенсионеры “проедят” портфели за 10 лет!
Возможно, вы уже догадались, что вы сделали не так.

Бенген в 1994 году метко попал. В 2004 году действительно раздувался пузырь, коих свет не видел (ипотеки в США). С началом трехлетней рецессии он промахнулся на 1 год: начали говорить о рецессии в 2007 году. Действительно, в начале 2008 инфляция во всем мире была рекордной. ФРС действительно печатала деньги и снизила ставку до нуля. Единственное, в чем ошибся Бенген — в том, что силе и продолжительности инфляции. А пенсионный советник из истории ошибся в том, что поставил фиксированную сумму снятия (с одинаковой ежегодной индексацией), позабыв о том, что инфляция может сильно скакать. Так какой выход из ситуации видит Бенген? Нужно снимать не фиксированную рассчитанную сумму, индексируя её, нужно снимать фиксированный процент от объема портфеля! Такой подход защитит пенсионера от периодов с инфляцией, дефляцией, стагфляцией, и любой другой -фляцией. По крайней мере, такой вывод позволяют сделать исторические данные.

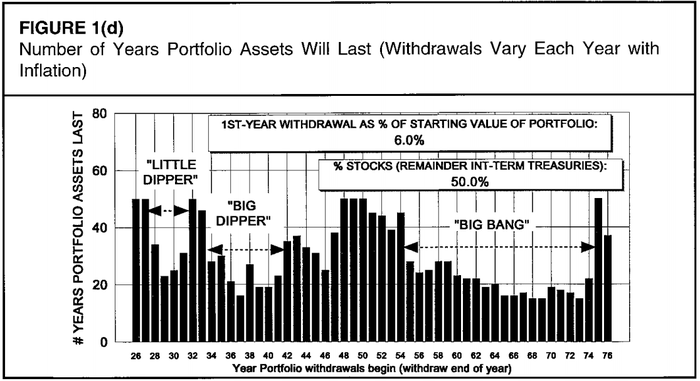
Бенген проанализировал 70-летний набор данных, и определил, что худшими периодами выхода на пенсию с портфелем “50/50 облигации/акции” были три периода (он учился на астронома, отсюда и названия событий):

Малая Медведица, 1929-1931. Это удивительно, но этот период — наименее плохой из трех. Акции упали мощно. Но облигации выросли. А главным “смягчающим” фактором (для пенсионера, а не для экономики) была мощная дефляция. Деньги дорожали, а не дешевели. На поддержание того же уровня жизни требовалось меньше денег с годами.

Большая Медведица, 1937-1941. Средний из худших периодов. Опять же, акции падали, облигации росли, инфляция была, но низкая.

Большой Взрыв, 1973-1974. Наихудший период для только вышедшего на пенсию пенсионера! Период стагфляции. Акции падали, но при этом был всплеск инфляции, и деньги обесценивались! Запомните, это худшее, что можно придумать в момент перехода от стадии накопления к стадии “проедания”. Да, хуже Великой Депрессии.

“Большая Медведица” (Big Dipper) и “Малая Медведица” (Little Dipper) в контексте кризисов — это игра слов. Dipper — ковш, близко к Dip — дно рынка, помним “buy the dip”, да? 😉 Малое дно, большое дно, ну вы поняли.

Все остальные периоды до 1994 г. не были такими плохими, несмотря на постоянные кризисы и обвалы. Всё это пыль в глаза.

Сценарий 1: 50/50 Акции/Облигации, вывод 3% от портфеля в год

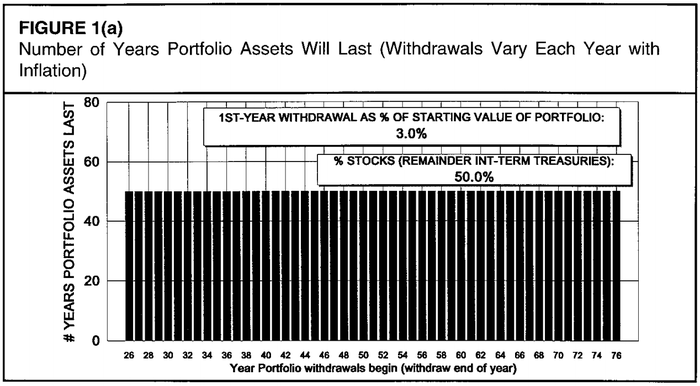
Бенген не считал дальше 50 лет, но многие периоды улетали в стратосферу. Это не так важно, и в век когда не было Экселя, это было роскошью в части временных затрат на расчеты. Вывод 3% от объема портфеля безопасен во все периоды, даже самые плохие, с 1926 по 1976 год.

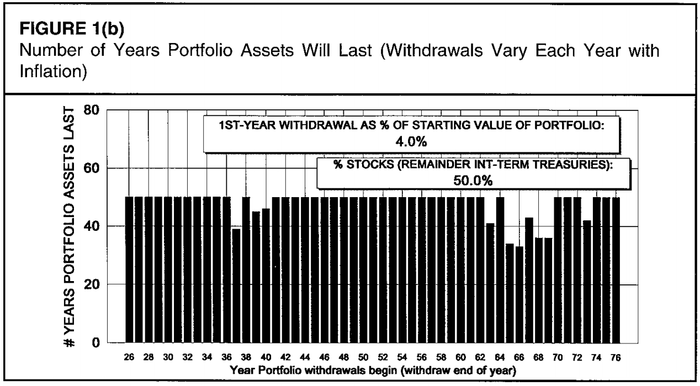
Сценарий 2: 50/50 Акции/Облигации, вывод 4% от портфеля в год

Этот сценарий безопасен в периоды типа Великой Депрессии, но при выходе на пенсию накануне кризиса со стагфляцией портфеля будет хватать всего на 35 лет.

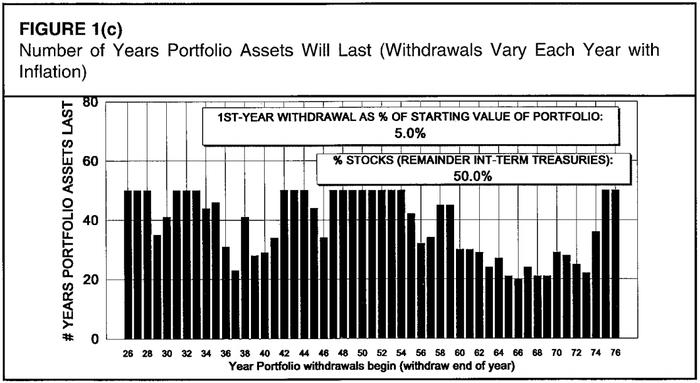
Сценарий 3: 50/50 Акции/Облигации, вывод 5% от портфеля в год

Весь период с 1963 по 1973 годы — плохой, денег хватает на 20 лет, да и Великую Депрессию появляются провалы.

Сценарий 4: 50/50 Акции/Облигации, вывод 6% от портфеля в год

Периодов, когда портфель не “проедается” меньше, чем периодов, когда он “проедается”. Никуда не годится.

Сценарий 2 (4%) — оптимальный. Вот так и повелось. Но это ещё не конец.

ВЛИЯНИЕ АЛЛОКАЦИИ АКТИВОВ

Приведу два графика — оригинальный от 1994 и график Merrill Lynch/BofA из другого хорошего исследования, которое я тоже переведу как только дойдут руки:

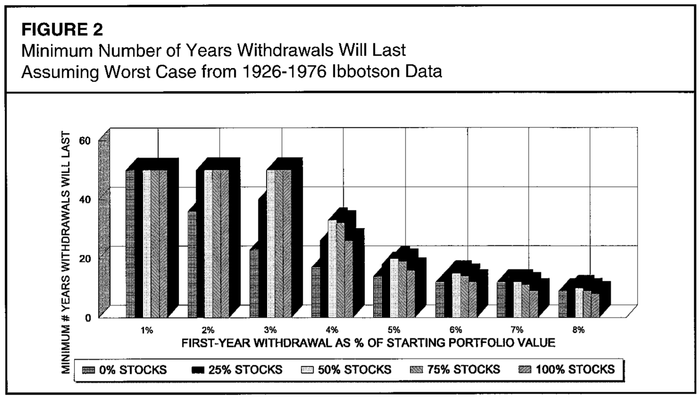
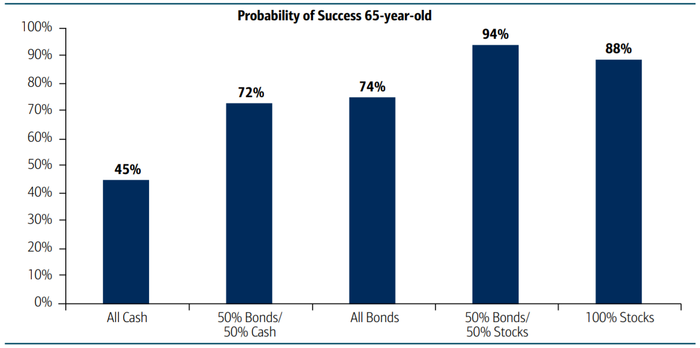
Минимальное количество лет, которое мог бы продержаться ваш портфель при самом худшем стечении обстоятельств

Вероятность не «проесть свой портфель» при применении Правила 4% и при различной аллокации активов от 100% в кэше до 100% в акциях

Бенген промоделировал все доступные ему периоды с разным процентом снятия средств и с разной аллокацией активов:

0% акций, 100% облигаций

25% акций, 75% облигаций

50% акций, 50% облигаций

75% акций, 25% облигаций

100% акций, 0% облигаций

На графике выше — наихудший из возможных результатов. Давайте сразу обратимся к нашим 4%, и к цитате из исследования Бенгена:

Столбцы «0% акций» и «25% акций» всегда короче других. График подтверждает то, что мы и так уже знаем — превосходство доходности акций по сравнению с облигациями на длительных периодах. Содержание слишком малой доли акций в портфеле укорачивает минимальный срок жизни портфеля.
50/50 кажется почти оптимальной аллокацией для портфеля, из которого снимаются пенсионные средства: у такого портфеля самые высокие показатели долговечности.

Незначительно отстает по долговечности и портфель 75/25 в пользу акций. Можно сделать несложный вывод:

«Больше акций» лучше, чем «меньше акций» для портфеля на этапе, когда он кормит вас.

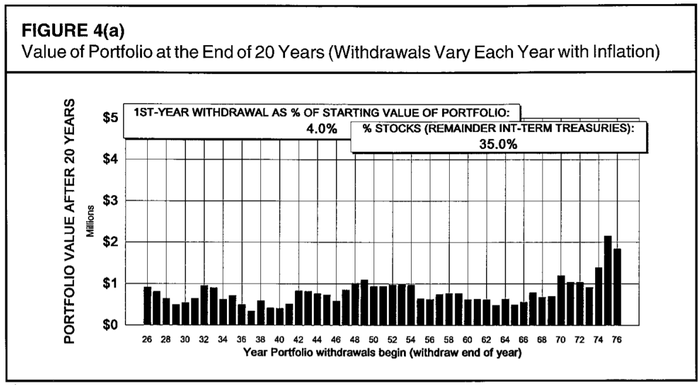
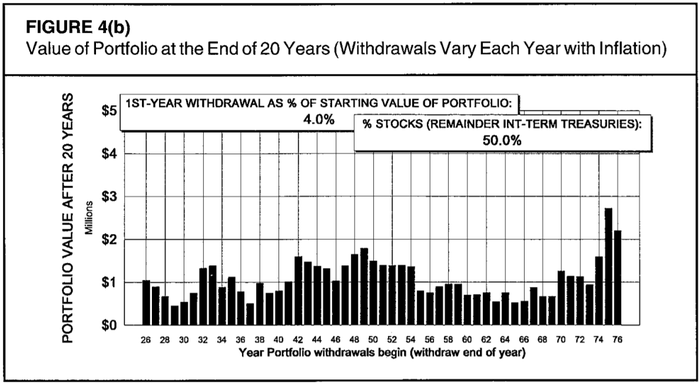
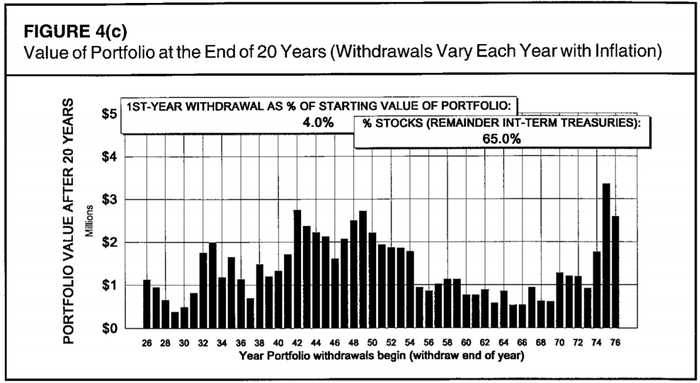
На следующих графиках указана рассчитанная через 20 лет стоимость портфеля размером 1 млн долларов, из которого изымались средства каждый год по Правилу 4%. Разница портфелей — только в соотношении «акции/облигации», где доля акций от верхнего к нижнему: 35%, 50%, 65%, 75%. Привожу графики подряд, для того чтобы наглядно показать ключевую разницу.

Для худших периодов через 20 лет после выхода на пенсию портфель оказывался бы примерно в той же точке, независимо от доли акций в нём. Десятью тысячами больше, десятью тысячами меньше. Но в случае «удачного» выбора времени для выхода на пенсию, бонус за большую долю акций в портфеле — просто огромный. Разница составляет миллионы долларов!

Вот что пишет по этому поводу Бенген в своем исследовании:

Разбирая все это, я думаю, что уместно советовать принять долю акций близко к 75 процентам, и ни в коем случае не менее 50 процентов. Доля акций ниже 50 процентов контрпродуктивна, поскольку такая аллокация снижает количество накопленного богатства одновременно со снижением долговечности портфеля. Где-то между 50/50 и 75/25 должна быть «зоной комфорта» любого пенсионера.

Под «черными дырами» Бенген подразумевает наихудшие сценарии из тех, что были. Например, клиент, который вышел на пенсию в 1929 году с $500’000 с 75/25 (на самой макушке пузыря перед Великой Депрессией) столкнулся бы с сокращением портфеля до менее чем $200’000 на конец 1932 года. Всего через 3 года! Изъятия из портфеля составляли бы уже 7,6% от стоимости портфеля в год. Хотя в абсолютных показателях эти изъятия бы сократились из-за мощнейшей дефляции: с $20’000 в 1929 г. до $15’300 в 1932 г. В ситуации, когда акции показали такой ужасный результат, да ещё и так рано, может возникнуть соблазн переложиться в облигации с целью спасения того что осталось. Но это было бы самым неправильным поступком!

Такое решение, принятое 31 декабря 1932 года, после долгих лет падения акций привело бы к тому, что в 1946 году его деньги бы закончились. Если бы этот клиент ничего не делал, он бы пережил Великую Депрессию, а его портфель к 1992 году вырос бы до 1,7 млн долларов, несмотря на продолжающиеся снятия по Правилу 4% и отсутствию каких-либо пополнений.

А что бы было, если бы этот клиент проявил смелость, и несмотря на огромное снижение портфеля, пошел бы в противоход «плохим» мыслям? Что было бы, если бы пенсионер сказал «а к черту, перевожу все облигации в акции»? Если бы он сделал это и сохранил аллокацию 100/0 до конца 1992 года, то у него было бы на счету $42 млн! Настолько мощно было последующее ралли в акциях, несмотря на многочисленные кризисы после.

Моделирование других плохих ситуаций показала такой же результат. Ситуация с 1929 годом здесь наиболее показательна, т.к. это было самым крупным падением в акциях.

Такое решение — перевод облигаций в акции в момент, когда акции, кажется, обречены на полный крах — может оказаться слишком сложным. Что ж, есть альтернативное решение, которое тоже показало эффективность: «затянуть пояса». Снижение объема снятия средств в кризисные пару лет, когда вам страшно за свой портфель, даже небольшое, оказывает значительный эффект на результат.

А вот решение продать упавшие акции и выйти в кэш (или купить облигации) в момент когда акции упали, в опасении, что они упадут ещё сильнее — КОНТРПРОДУКТИВНО.

На другом конце этого спектра расположились «Звёзды» — так Бенген назвал пенсионеров, которым повезло выйти на пенсию в период рыночного бума. Их проблемы и мысли зачастую прямо противоположны (я напомню, Бенген был пенсионным консультантом — это как раз тот человек, который выслушивал разных людей, с разными ситуациями, вышедших на пенсию в разные годы, и он лучше всех знает эмоции и тех, и других). Чаще всего таких людей посещают две мысли: увеличить свой уровень жизни, начав забирать из портфеля больше (ведь он так вырос!), и продать все свои облигации, переложив деньги в акции (ведь они так хорошо растут, упущенная прибыль!).

Рассмотрим обратный пример: человек вышел на пенсию с $500’000 в 1958, применив Правило 4%, и корректируя на инфляцию каждый год свои снятия. Рынок буйно рос 9 лет, в среднем на 12,9% в год, а инфляция была низкой, 1,8% в год. В итоге, получилась ситуация, при которой пенсионер снимал всего 2,3% от своего портфеля на 9-ый год, а в портфеле уже более 1 млн долларов. Он решил повысить свои снятия до $40’000. Немного неудачный 1969 не спутал карты, а потом настал тот самый «Большой взрыв» — 1973-1974 гг. Мало того, что сам портфель просел, так еще и мощная инфляция заставляла наращивать снятия, ведь к хорошему привыкаешь быстро, и за 6 лет пенсионер уже привык к новому уровню жизни. В итоге получилось, что он снимал уже 8% в 1975 году! «Упавшая звезда» может запустить необратимый процесс превращения в «черную дыру», если примет в таком случае ещё одно неправильное решение: попытается сохранить капитал, уменьшив долю акций.

А выход из ситуации здесь абсолютно такой же, как и в рассказе о «черной дыре»: или наоборот — нарастить долю акций до 100%, или «затянуть пояса», снизив уровень снятий. Оба решения помогли бы выправить ситуацию с сокращающимся портфелем.

Под «астероидами» Бенген подразумевает всё то множество пенсионеров, которые находились в середине этого распределения. Их большинство. Их истории не так интересны. Ведь правило 4% для них работает прекрасно, им не нужно ничего предпринимать. У кого-то лучше складывалось первое десятилетие и хуже — второе десятилетие. У кого-то наоборот. Совет для них всех должен быть всегда одинаковым: stay the course — придерживайтесь изначально заданного курса.

Что там с пенсионной системой в России?

1. Не секрет, что он жутко дефицитный, и вкладывать в ценные бумаги нечего.

2. Однако, у нас есть та самая накопительная часть пенсии. Она ничтожно мала и заморожена, так что обычно с ней никто не считается. Но интересен сам принцип, которого придерживаются наши регуляторы в этой сфере. А принцип таков, что НПФ’ам запрещено на законодательном уровне держать высокую долю акций. НПФ’ы держат практически все ваши накопления в рублевых облигациях. Даже ничтожных шансов на хорошую накопительную часть нет. Об этом я писал отдельный пост, в котором показывал доходность НПФ, в котором хранятся мои деньги.

3. Складывается ощущение, что пенсионная система России не думает длинными горизонтами, совершая крайне нелогичные шаги. Один за другим.

4. Вспоминается другой подход — норвежский — резко критикуемый комментаторами на Пикабу. Несмотря на результаты норвежцев (хорошие результаты), на Пикабу их подход воспринимается как дерьмовый, безответственный, лудоманский. Норвежская пенсионная система имеет аллокацию активов 70/27/3 — акции/облигации/недвижимость.

Зачем мне всё это нужно? Ну вообще-то, я собрался на пенсии жить, а не выживать. Мне 31 год, но уже сейчас меня волнует ответ на вопрос «как жить в старости?» Более того, с нынешними параметрами дохода/сбережений, у меня есть все шансы уйти на пенсию в 43 года, а не в 65. С пенсией раз в 5-6 большей, чем государственная. Как я к этому иду, и как я веду свой собственный мини-пенсионный фонд (нет, никого туда не принимаю ни за какие деньги, там только наши семейные сбережения и больше ничьи) в условиях суровой российской реальности — я рассказываю в своем блоге в Телеграм или здесь на Пикабу. Собственно, оттуда этот огромный текст.

Источник