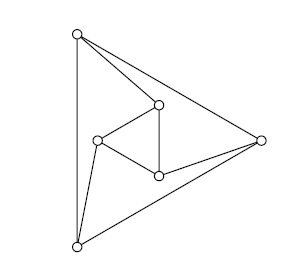
Любые два города страны соединены дорогой

Задача 1: odin Докажите по индукции, что в графе с n вершинами чётное число вершин с нечётной степенью.

Задача 2: odnostor В стране любые два города соединены дорогой с односторонним движением. Доказать, что можно проехать по всем городам, побывав в каждом по одному разу.

Решение: Индукционный переход. Уберём произвольный город A. По индукционному предположению оставшуюся часть можно обойти, пусть этот путь начинается с города B. Если дорога между A и B ведёт в B, то можно из A переехать в B, и проехать оттуда по оставшимся городам. Если же эта дорога ведёт в A, то рассмотрим последний город на пути (C). Если дорога между A и C ведёт в A, то искомый маршрут – B–…–C–A. Иначе – рассмотрим первый город на пути, в который ведёт дорога из A. (назовём его D, а предыдущий – E) и воспользуемся маршрутом B–…–E–A–D–…–C.

Задача 3: Усадьбы любых двух джентльменов в графстве Вишкиль соединены либо водным (лодочка), либо сухопутным (карета) сообщением. Докажите, что можно закрыть один из видов транспорта так, чтобы любой джентльмен мог по-прежнему добраться до любого другого.

Решение: Переход. Уберём произвольный город A. По индукционному предположению теперь можно добраться от одного города в другой с помощью лодочки или кареты. Пусть, для определённости, можно добраться с помощью лодочки). Если из A можно добраться водным путём хотя бы в один город, то можно добраться и до любого другого города. Если же из A во все остальные города ездит карета, то из любого города до любого другого можно добраться сухопутным путём через город A.

Задача 4: В некоторой стране каждый город соединён с каждым дорогой с односторонним движением. Докажите, что найдется город, из которого можно добраться в любой другой не более чем с одной пересадкой.

Решение: Индукция по числу городов. База очевидна. Для доказательства индукционного перехода удалим сначала один из городов (назовём его A). В силу индукционного предположения есть город B с требуемым свойством. Если из B в A ведёт дорога, то город B искомый. Если же дорога ведёт из A в B, то рассмотрим все города, в которые ведёт дорога из B. Если хоть из одного из них ведёт дорога в A, то город B снова искомый. В противном случае искомым является город A.

Задача 5: Доказать, что после окончания однокругового турнира по теннису его участников можно выстроить в ряд так, что каждый выиграл у следующего за ним в этом ряду.

Решение: Это переформулировка задачи о существовании пути в полном ориентированном графе.

Задача 6: В графе с 2n вершинами n² + 1 ребро. Докажите, что в нем есть три вершины, попарно соединённые ребрами.

Решение: Индукционный переход. Пусть утверждение верно для произвольного графа с 2n вершинами. Докажем, что оно верно и для графа с 2(n + 1) вершинами. Рассмотрим произвольные две вершины A и B. Если существует вершина C, из которой идут рёбра и в A и в B, то треугольник нашёлся. Если же такой вершины нет, то из вершин A и B ведёт не более 2n рёбер. Поэтому, если убрать из графа вершины A и B, то останется 2n вершин и не менее чем (n + 1)² – 2n = n² + 1 рёбер и по индукционному предположению в оставшейся части графа найдётся треугольник.

Задача 7: В компании из n человек среди любых четверых есть знакомый с остальными троими. Доказать, что есть человек, который знает всех остальных.

Источник

Любые два города страны соединены дорогой

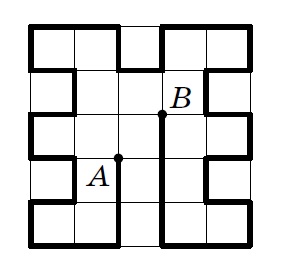
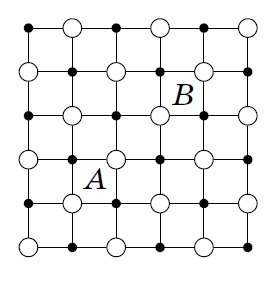
Двигаясь по этому пути, турист пройдёт 34 улицы (улицей мы называем отрезок между двумя соседними перекрёстками). Докажем, что более длинный маршрут невозможен. Всего в Старом городе 36 перекрёстков. Всякий раз, когда турист проходит очередную улицу, он попадает на новый перекрёсток. Таким образом, больше чем 35 улиц турист пройти не сможет (начальный перекрёсток A не считается). Покажем, что посетить 35 перекрёстков (и, следовательно, пройти 35 улиц) любознательный турист тоже не сможет. Для этого раскрасим перекрёстки в чёрный и белый цвета в шахматном порядке.

Всякий раз, проходя улицу, турист попадает на перекрёсток другого цвета. И отель, и вокзал расположены на белых перекрёстках. Поэтому любой маршрут содержит чётное число улиц, а число 35 нечётно.

б) Если в матче одна из команд ожержит победу, то в сумме за матч будет разыграно 3 очка; если же ни одна из команд не выиграет, то в сумме будет разыграно два очка. Ясно, что можно добиться того, чтобы в каждом матче было разыграно 2 очка — каждый матч закончиться ничьей. Тогда будет разыграно всего 16·15·2 = 480 очков. Максимальное число будет разыграно, когда в каждом матче одна из команд выиграет. В этом случае будет разыграно 16·15·3 = 720 очков.

Источник

Любые два города страны соединены дорогой

В некоторой стране каждые два города соединены либо авиалинией, либо железной дорогой. Докажите, что
а) можно выбрать вид транспорта так, чтобы от каждого города можно было добраться до любого другого, пользуясь только этим видом транспорта;
б) из некоторого города, выбрав один из видов транспорта, можно добраться до любого другого города не более чем с одной пересадкой (пользоваться можно только выбранным видом транспорта);
в) каждый город обладает свойством из пункта б);
г) можно выбрать вид транспорта так, чтобы пользуясь только им, можно было добраться из каждого города до любого другого не более чем с двумя пересадками.

Решение

а) Первый способ. Пусть из некоторого города A нельзя попасть в некоторый город B по железной дороге. Рассмотрим множество M всех городов, в которые можно попасть из города A по железной дороге. Множество городов, не входящих в M, обозначим N. Множество N непусто, поскольку в нём содержится город B. Ясно, что из городов множества M нельзя попасть в города множества N по железной дороге.
Докажем, что из каждого города в любой другой можно попасть авиарейсами.
Если один из городов принадлежит M, а другой – множеству N, то между ними есть прямая авиалиния.
Пусть два города принадлежат M. Тогда из первого города можно попасть авиарейсом в некоторый город множества N, а оттуда (также самолётом) – во второй город.
Аналогично рассматривается случай, когда оба города принадлежат N.
Второй способ. См. г).

в) Пусть для города X это не так: есть город A, в который из X нельзя долететь за два «хода», и город B, в который из X нельзя доехать на поезде за два «хода» (значит, X и B связаны авиалинией). Пусть A и B связаны авиалинией. Тогда в X из A в можно добраться по воздуху с пересадкой в B. Противоречие.
Аналогично к противоречию приводит и предположение о том, что A и B связаны железной дорогой.

г) Пусть из A в нельзя долететь за три «хода», а из C в D нельзя доехать на поезде за три «хода». Тогда A и B связаны железной дорогой, а C и D – авиалинией.
Пусть A и C связаны железной дорогой. Тогда B и D связаны авиалинией (иначе был бы ж/д маршрут CABD), а A и D – железной дорогой (иначе есть авиамаршрут BDA). Противоречие: есть ж/д маршрут CAD.
Аналогично к противоречию приводит и предположение о том, что A и C связаны авиалинией.

Источники и прецеденты использования

книга
Автор	Генкин С.А., Итенберг И.В., Фомин Д.В.
Год издания	1994
Название	Ленинградские математические кружки
Издательство	Киров: «АСА»
Издание	1
глава
Номер	13
Название	Графы-2
Тема	Теория графов
задача
Номер	036

Проект осуществляется при поддержке и .

Источник

Любые два города страны соединены дорогой

Решение

Источники и прецеденты использования

книга
Автор	Генкин С.А., Итенберг И.В., Фомин Д.В.
Год издания	1994
Название	Ленинградские математические кружки
Издательство	Киров: «АСА»
Издание	1
глава
Номер	13
Название	Графы-2
Тема	Теория графов
задача
Номер	036

Проект осуществляется при поддержке и .

Источник

Любые два города страны соединены дорогой

Задача 41:

Дима, приехав из Врунляндии, рассказал, что там есть несколько озер, соединенных между собой реками. Из каждого озера вытекают три реки, и в каждое озеро впадают четыре реки. Докажите, что он ошибается.

Решение:

Указание: Общее количество «втекающих» рек должно быть равно общему количеству «вытекающих» рек.

Задача 42:

В некоторой стране есть столица и еще 100 городов. Некоторые города (в том числе и столица) соединены дорогами с односторонним движением. Из каждого нестоличного города выходит 20 дорог, и в каждый такой город входит 21 дорога. Докажите, что в столицу нельзя проехать ни из одного города.

Решение:

Пусть в столицу входит a дорог. Тогда общее число «входящих дорог равно 21 100 + a, а общее количество «выходящих» дорог не больше 20 100 + (100 – a). Поэтому 21 100 + a ≤ 20 100 + (100 – a), то есть 2a ≤ 0. Таким образом, a = 0.

Задача 43:

В некотором государстве каждый город соединен с каждым дорогой. Сумасшедший король хочет ввести на дорогах одностороннее движение так, чтобы выехав из любого города, в него нельзя было вернуться. Можно ли так сделать?

Решение:

Занумеруйте города и направьте движение от городов с меньшими номерами к городам с большими номерами.

Задача 44:

Докажите, что на ребрах связного графа можно так расставить стрелки, чтобы из некоторой вершины можно было добраться по стрелкам до любой другой.

Решение:

Рассмотрите сначала вершины, соединенные с любой фиксированной вершиной A, затем – новые вершины, соединенные с ними и т.д. При этом ребра, соединяющие добавляемые вершины с уже рассмотренными, ориентируем в направлении к новым вершинам.

Задача 45:

В связном графе степени всех вершин четны. Докажите, что на ребрах этого графа можно расставить стрелки так, чтобы выполнялись следующие условия:

а) двигаясь по стрелкам, можно добраться от любой вершины до любой другой;

б) для каждой вершины числа входящих и выходящих ребер равны.

Решение:

Рассмотрим эйлеров цикл, проходящий по всем ребрам графа, и ориентируем все ребра в соответствии с порядком прохождения цикла.

Задача 46:

На ребрах связного графа расставлены стрелки так, что для каждой вершины числа входящих и выходящих ребер равны. Докажите, что двигаясь по стрелкам, можно добраться от любой вершины до любой другой.

Решение:

Докажите, что существует замкнутый путь вдоль стрелок, проходящий по каждому ребру ровно один раз.

Задача 47:

В некоторой стране каждый город соединен с каждым дорогой с односторонним движением. Докажите, что найдется город, из которого можно добраться в любой другой.

Решение:

Индукция по числу городов. База очевидна. Для доказательства индукционного перехода удалим сначала один из городов. В силу индукционного предположения есть город А с требуемым свойством. Вспомним теперь про удаленный город. Если в него ведет хотя бы одна дорога, то город А – искомый. В противном случае сам удаленный город удовлетворяет требуемому свойству.

Задача 48:

Несколько команд сыграли между собой круговой турнир по волейболу. Будем говорить, что команда А сильнее команды В, если либо А выиграла у В, либо существует команда С такая, что А выиграла у С, а С – у В.

а) Докажите, что есть команда, которая сильнее всех.

б) Докажите, что команда, выигравшая турнир, сильнее всех.

Решение:

Если существует команда, выигравшая и у команды-победительницы, и у всех команд, проигравших победителям, то у такой команды очков больше, чем у победителей турнира, что невозможно.

Задача 49:

В одном государстве 100 городов и каждый соединен с каждым дорогой с односторонним движением. Докажите, что можно поменять направление движения на одной дороге так, чтобы от любого города можно было доехать до любого другого.

Решение:

База – для трех городов. Для доказательства индукционного перехода удалите город, имеющий и входящие и выходящие дороги.

Задача 50:

20 команд сыграли круговой турнир по волейболу. Докажите, что команды можно занумеровать числами от 1 до 20 так, что 1-я команда выиграла у 2-й, 2-я – у 3-й, …, 19-я у 20-й.

Задача 51:

Какие-то две команды набрали в круговом волейбольном турнире одинаковое число очков. Докажите, что найдутся команды А, В и С такие, что А выиграла у В, В выиграла у С, а С выиграла у А.

Решение:

Пусть А и В набрали одинаковое количество очков, причем В выиграла у А. Тогда если для любой команды С, у которой выиграла А, выиграла и В, то у В должно быть очков больше, чем у А. Следовательно, есть команда С такая, что А выиграла у С, а С выиграла у В.

Задача 52:

В некотором государстве 101 город.

а) Каждый город соединен с каждым дорогой с односторонним движением, причем в каждый город входит 50 дорог и из каждого города выходит 50 дорог. Докажите, что из любого города можно доехать в любой другой, проехав не более, чем по двум дорогам;

б) Некоторые города соединены дорогами с односторонним движением, причем в каждый город входит 40 дорог и из каждого города выходит 40 дорог. Докажите, что из любого города можно добраться до любого другого, проехав не более, чем по трем дорогам.

Решение:

Пусть из города А нельзя доехать до города В. Рассмотрите города, в которые входят дороги из А, и города, из которых выходят дороги в В. б) Вычислите общее количество дорог, выходящих из первой группы городов. Заметьте, что этих дорог достаточно много для того, чтобы хотя бы одна из них кончалась в городе из второй группы.

Задача 53:

В стране Ориентация на всех дорогах введено одностороннее движение, причем из любого города в любой другой можно добраться, проехав не более, чем по двум дорогам. Одну дорогу закрыли на ремонт так, что из каждого города по-прежнему можно добраться до каждого. Докажите, что для любых двух городов это можно сделать, проехав не более, чем по трем дорогам.

Решение:

Пусть удалено ребро между вершинами А и В. Выберем две произвольные вершины. Рассмотрите три случая: обе эти вершины не совпадают с А или В, одна из них совпадает с А или с В, эти вершины – А и В.

Источник